PROVE TWO TRIANGLES ARE SIMILAR AND FIND THE MISSING LENGTHS

How to prove two triangles are similar ?

If two triangles are equiangular then they are similar. Similar triangles have corresponding sides in the same ratio.

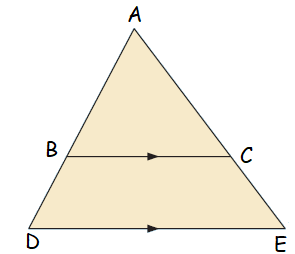
In triangles ABC and ADE. it is given BC is parallel to DE

<ABC  =  <ADB

<BAC  =  <DAE

Ratios of corresponding sides,

AC/AE  =  BC/DE  =  AB/AD

By applying the known values here, we can find the unknow.

In each of the following figures, establish that a pair of triangles is similar, and find x.

Problem 1 :

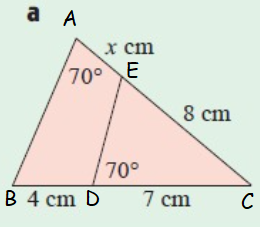
Solution :

In triangle ABC and in EDC.

<BAC  =  <DEC

<BCA  =  <DCE

So, the triangles ABC and EDC are similar.

BC/EC  =  AB/ED  =  AC/DC

(4+7)/8  =  AB/ED  =  (x+8)/7

11/8  =  (x+8)/7

77  =  8(x+8)

77  =  8x+64

8x  =  77-64

8x  =  13

x  =  13/8

x  =  1.625 cm

Problem 2 :

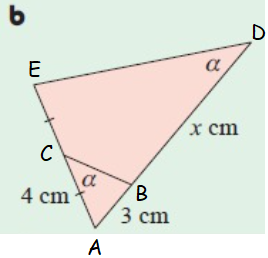
Solution :

<ACB  =  <ADE

<CAB  =  <EAD

So, the triangles ABC and AED are similar.

AB/AE  =  BC/ED  =  AC/AD

3/(4+4)  =  BC/ED  =  4/(3+x)

3/8  =  4/(3+x)

3(3+x)  =  32

9+3x  =  32

3x  =  32-9

3x  =  23

x  =  23/3

x  =  7.66 cm

If the given triangles are similar, find the value of x.

Problem 3 :

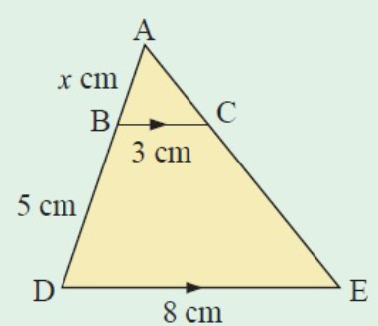
Solution :

BC/DE  =  AC/AE  =  AB/AD

3/8  =  x/(x+5)

3(x+5)  =  8x

3x+15  =  8x

8x-3x  =  15

5x  =  15

x  =  15/5

x  =  3

Problem 4 :

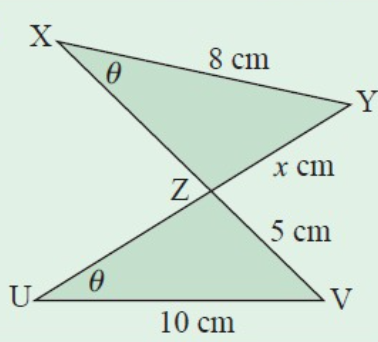
Solution :

ZV/ZY  =  UV/XY

5/x  =  10/8

5(8)  =  10x

40  =  10x

x  =  4

Problem 5 :

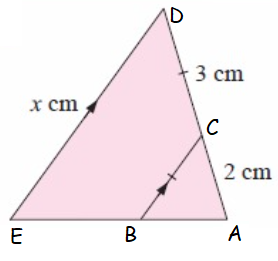
Solution :

BC/ED  =  AB/EA  =  AC/DA

BC/x  =  AB/EA  =  2/5

BC/x  =  2/5

3/x  =  2/5

5(3)  =  2x

15  =  2x

x  =  15/2

x  =  7.5 cm

Problem 6 :

Two triangles are shown below.

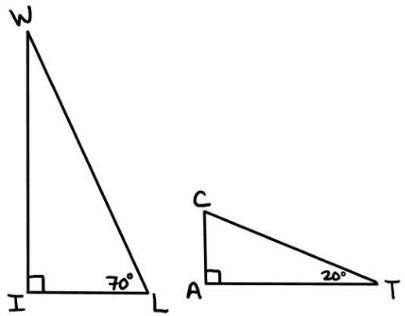
a) Find the missing angle in each triangle. How does this show that the triangles are similar?

b) If 𝑾𝑰 = 𝟗.𝟒 and 𝑾𝑳 = 𝟏𝟎. Find the side 𝑰𝑳 using the Pythagorean Theorem (to one decimal)

c) If the scale factor from 𝚫𝑾𝑰𝑳 to 𝚫𝑻𝑨𝑪 is ½, find all the missing sides of triangle 𝚫𝑻𝑨𝑪.

Solution :

a)

Since we have two angles measures are the same. The triangles are similar.

b)  𝑾𝑰 = 𝟗.𝟒, 𝑾𝑳 = 𝟏𝟎

Using Pythagorean theorem, 

WL² = WI² + IL²

10² = 9.4² + IL²

100 - 88.36 = IL²

IL = √11.64

IL = 3.41

c) 1/2 of sides of the triangle WIL = sides of triangle ACT

(1/2) of WL = CT

(1/2) of 10 = CT

CT = 5

Problem 7 :

A 6 ft tall tent standing next to a cardboard box casts a 9 ft shadow. If the cardboard box casts a shadow that is 16 ft long then how tall is it ?

Solution :

Height of tent = 6ft

height of cardboard = 9 ft

Length of shadow of cardboard = 16 ft

length of shadow of tent = x

6 : 9 = 16 : x

6/9 = 16/x

6x = 16(9)

x = 144/6

x = 24 ft

So, length of shadow of tent is 24 ft.

Problem 7 :

When a Ferris wheel casts a 20 meters shadow, a man 1.8 meters tall casts a 2.4 meter shadow. How tall is this Ferris wheel ?

Solution :

Length of shadow of Ferris wheel = 20 meters

Height of man = 1.8 meters

Length of shadow of man = 2.4 meters

Height of Ferris wheel = x

x : 20 = 1.8 : 2.4

x/20 = 1.8/2.4

2.4x = 1.8(20)

x = 1.8(20) / 2.4

= 15 meters

So, the height of Ferris wheel is 15 meters.

Problem 8 :

A photographer measuring four inches wide and five inches long is enlarged to make a wall mural. If the mural is 120 inches wide, how long is the mural ?

Solution :

Length of original picture = 5 inches

Width of original picture = 4 inches

Width of mural = 120 inches

Length of mural = x

5 : 4 = x : 120

5/4 = x/120

5x = 120(4)

x = 120(4)/5

x = 24(4)

= 96 inches

So, length of mural is 96 inches.

Problem 9 :

A 9 foot ladder leans against a building six feet above the ground. At what height would a 15 foot ladder touch the building if both ladders against the same angle with the ground ?

Solution :

Length of ladder = 9 foot

The distance between foot of the building and top of ladder = 6 foot

Length of ladder = 15 foot

The distance between foot of the building and top of ladder = x

9 : 6 = 15 : x

9/6 = 15/x

9x = 15(6)

x = 15(6)/9

x = 10 foot

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.