PROVING BASIC PROPORTIONALITY THEOREM IN GIVEN TRIANGLE

Example 1 :

ABCD is a quadrilateral with AB parallel to CD. A line drawn parallel to AB meets AD at P and BC at Q. Prove that AP/PD = BQ/QC.

Solution :

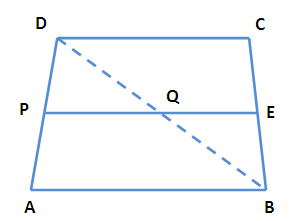
Join BD by intersecting the line PQ at the point Q.

In triangle DAB, PE and AB are parallel, by using “Thales theorem”

AP/PD = BE/ED ----(1)

In triangle BCD EQ and DC are parallel, by using “Thales theorem”

BE/ED = BQ/QC ----(2)

(1)  =  (2)

AP/PD = BQ/QC

Example 2 :

In t he figure, PC and QK are parallel BC and HK are parallel, if AQ = 6 cm, QH = 4 cm, HP = 5 cm, KC = 18 cm, then find AK and PB.

Solution :

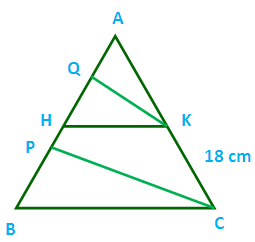
In triangle APC, the sides PC and QK are parallel.

By using “Thales theorem” we get

AQ/QP = AK/KC

QP = QH + HP

      = 4 + 5

  = 9 cm

6/9 = AK/18

AK = (6 x 18)/9

AK = 12 cm

In triangle ABC, the sides BC and HK are parallel,

By using “Thales theorem” we get

AH/HB = AK/KC

AH = AQ + QH

= 6 + 4

= 10

10/HB = 12/18

(10 x 18)/12 = HB

HB = 15 cm

Now we need to find the length of PB,

PB = HB – HP

= 15 – 5

= 10 cm

Example 3 :

In the figure DE is parallel to AQ and DF is parallel to AR prove that EF is parallel to QR.

Solution :

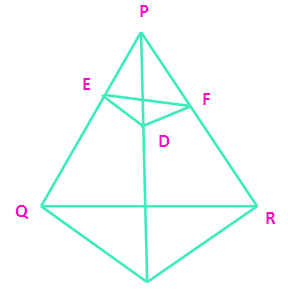
In triangle PQA, the sides DE is parallel to the side AQ.

By using “Thales theorem” we get

PE/EQ = PD/DA ----(1)

In triangle PAR, the sides DF is parallel to the side AR

By using “Thales theorem” we get

PD/DA = PF/FR ----(2)

(1) = (2)

PE/EQ = PF/FR

From this we can decide EF is parallel to QR in the given triangle PQR.

Example 4 :

In the figure the sides DE and AB are parallel and DF and AC are parallel. Prove that EF and BC are parallel.

Solution :

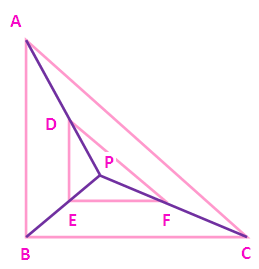
In triangle APB, the sides DE and AB are parallel.

PD/DA = PE/EB ----(1)

In triangle PAC, the sides DF and AC are parallel.

PD/DA = PF/FC ----(2)

(1) = (2)

PE/EB = PF/FC

Hence the sides EF and BC are parallel.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.