PROVING PROBLEMS INVOLVING TRIGONOMETRIC ANGLES FOR GRADE 11

Problem 1 :

Prove that

[cot(180° + θ)sin(90° - θ)cos(- θ)]/[sin(270° + θ)cot(180° + θ)tan (- θ)cosec(360° + θ)  =  cos²θcotθ 

Solution :

cot(180° + θ) : 

Lies in 3rd quadrant. For tan and cot we will have positive sign. 

cot(180° + θ)   =  -cotθ 

sin(90° - θ) :

Lies in 1^st quadrant. For all trigonometric ratios, we will have positive sign. 

sin(90° - θ)  =  cosθ 

cos(- θ) : 

According to the property cos (- θ)  =  cos θ

sin(270° + θ) :

Lies in 4^th quadrant. For cos and sec we will have positive sign. 

sin(270° + θ)  =  cosθ 

tan(- θ) :

According to the property tan(- θ)  =  -tanθ

cosec(360° + θ) :

Lies in 1^st quadrant. For all trigonometric ratios, we will have positive sign. 

cosec(360° + θ)  =  cosecθ 

Then, 

[cot(180° + θ)sin(90° - θ)cos(- θ)]/[sin(270° + θ)cot(180° + θ) tan (- θ)cosec(360° + θ) :

=   -cot θ cos θ cos θ /cos θ (-tan θ) cosec θ 

=  (cot θ cos θ) / (tan θ cosec θ)

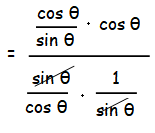
=   cos² θ cot θ

Problem 2 :

Find all the angles between 0° and 360°  which satisfy the equation sin²θ = 3/4.

Solution :

sin²θ  =  3/4

sinθ  =  √(3/4)

sinθ  =  √3/2

Hence the required angles are π/3 and 2π/3.

Problem 3 :

Show that sin² π/18 + sin² π/9 + sin² 7π/18 + sin² 4π/9  =  2.

Solution :

 sin²π/18 + sin²π/9 + sin²7π/18 + sin²4π/9 :

=  (sin π/18)² + (sin π/9)² + (sin 7π/18)² + (sin 4π/9)²

=  sin²10 + sin²20 + sin ²70 + sin²80

=  [cos(90 - 10)]² + [cos(90 - 20)]²  + sin ² 70 + sin² 80 

=  cos²80 + cos²70  + sin²70 + sin²80

 =  sin²80 + cos²80 + sin²70 + cos²70

 =  1 + 1

=  2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.