PROVING STATEMENTS ABOUT ANGLES

A true statement that follows as a result of other statements is called a theorem. All theorems must be proved. We can prove a theorem using a two-column proof. A two-column proof has numbered statements and reasons that show the logical order of an argument.

Properties of Angle Congruence

A proof which is written in paragraph form is called as paragraph proof.

Here is a paragraph proof for the Symmetric Property of Angle Congruence.

Paragraph Proof :

We are given that ∠A ≅ ∠B. By the definition of congruent angles, ∠A = ∠B.

By the symmetric property of equality, ∠B = ∠A.

Therefore, by the definition of congruent angles, it follows that

∠B  ≅  ∠A

Transitive Property of Angle Congruence

Prove the Transitive Property of Congruence for angles.

Solution :

To prove the Transitive Property of Congruence for angles, begin by drawing three congruent angles.

Label the vertices as A, B and C.

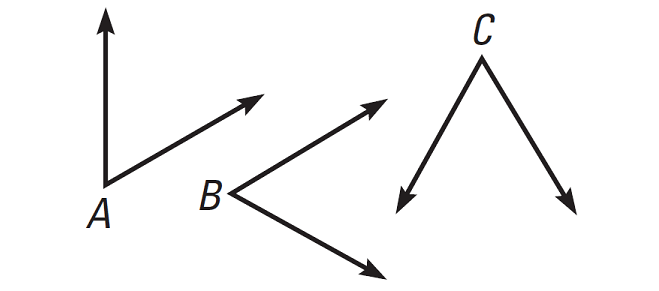
Given :

∠A ≅ ∠B

∠B ≅ ∠C

Prove :

∠A ≅ ∠C

Using Transitive Property

In the diagram shown below,

m∠3  =  40°, ∠1 ≅ ∠2, ∠2 ≅ ∠3

Prove m∠1 = 40°

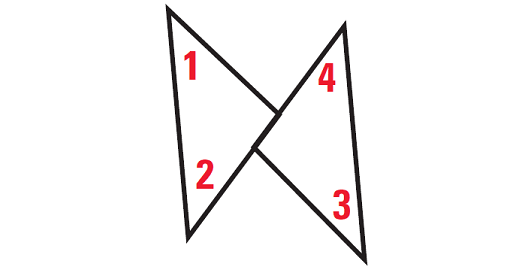
Solution :

Right Angle Congruence Theorem

All right angles are congruent.

Proof :

We can prove the theorem as shown below.

Given :  ∠1 and ∠2 are right angles

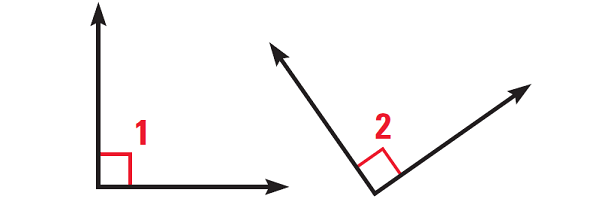
Prove ∠1 ≅ ∠2

Congruent Supplements Theorem

If two angles are supplementary to the same angle (or to congruent angles), then they are congruent.

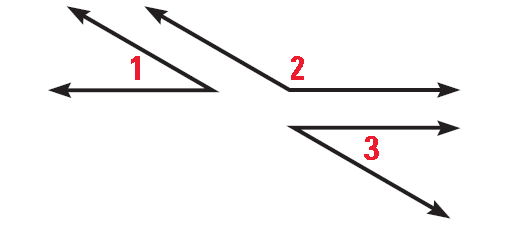
If m∠1 + m∠2  =  180° and m∠2 + m∠3  =  180°, then,

m∠1  ≅  m∠3

Proof :

We can prove the theorem as shown below.

Given :

∠1 and ∠2 are supplements,

∠3 and ∠4 are supplements,

∠1  ≅  ∠4

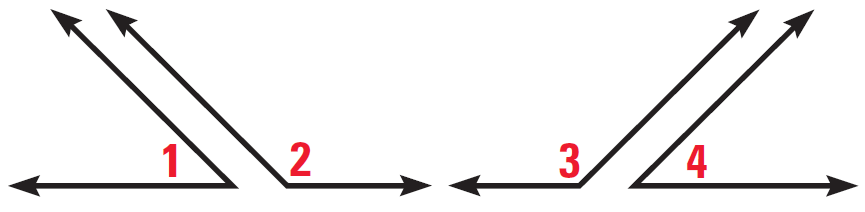
Prove ∠2 ≅ ∠3

Congruent Complements Theorem

If two angles are complementary to the same angle (or to congruent angles), then the two angles are congruent.

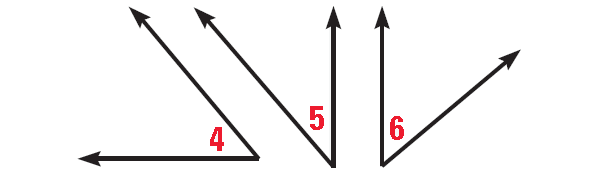
If m∠4 + m∠5  =  90° and m∠5 + m∠6  =  90°, then,

m∠4  ≅  m∠6

Linear Pair Postulate

If two angles form a linear pair, then they are supplementary.

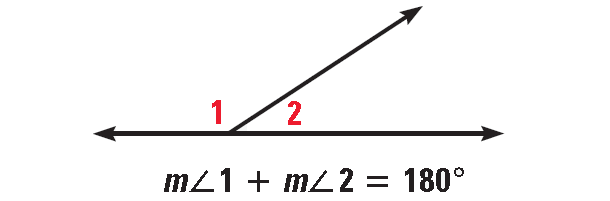
Using Linear Pairs

In the diagram shown below, m∠8 = m∠5 and m∠5 = 125°.

Prove that m∠7  =  55°.

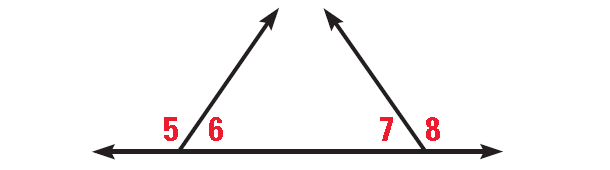
Using the transitive property of equality,

m∠8  =  125°

The diagram shows

m∠7 + m∠8  =  180°

Substitute 125° for m∠8.

m∠7 + 125°  =  180°

Subtract 125° from each side.

m∠7  =  55°

Vertical Angles Theorem

Vertical angles are congruent.

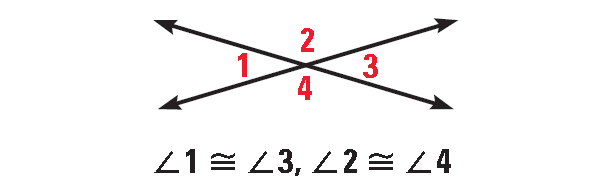
Proof :

Given :

m∠5 and m∠6 are a linear pair

m∠6 and m∠7 are a linear pair

Prove :

m∠5  ≅  m∠7

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.