WORKSHEET ON SLOPE OF A LINE
Question 1 :
What is the slope of a line whose inclination with positive direction of x -axis is 90°?
Question 2 :
What is the slope of a line whose inclination with positive direction of x -axis is 0°?
Question 3 :
Find the angle of inclination of a line whose slope is 1.
Question 4 :
Find the angle of inclination of a line whose slope is 0.
Question 5 :
Find the slope of a line joining the points (5, 5) with the origin.
Question 6 :
Find the slope of a line joining the following points :
(sinθ, -cosθ) and (-sinθ, cosθ)
Question 7 :
What is the slope of a line perpendicular to the line joining A(5, 1) and P where P is the mid-point of the segment joining (4, 2) and (-6, 4)?
Question 8 :
Show that the given points are collinear: (-3, -4), (7, 2) and (12, 5).
Question 9 :
If the three points (3, -1), (a, 3) and (1, -3) are collinear, find the value of a.
Question 10 :
The line through the points (-2, a) and (9, 3) has slope -½. Find the value of a.
Question 11 :
The line through the points (-2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24) . Find the value of x.
Question 12 :
Show that the given vertices form a right angled triangle and check whether its satisfies pythagoras theorem
(i) A(1, -4), B(2, -3) and C(4, -7)
(ii) L(0, 5), M(9, 12) and N(3, 14)
Question 13 :
Show that the given points form a parallelogram :
A(2.5, 3.5) , B(10,-4), C(2.5,-2.5) and D(-5,5)
Question 14 :
If the points A(2, 2), B(–2, –3), C(1, –3) and D(x, y) form a parallelogram then find the value of x and y.
Question 15 :
Let A(3, -4), B(9, -4), C(5, -7) and D(7, -7) . Show that ABCD is a trapezium.
Question 16 :
A quadrilateral has vertices A(-4, -2), B(5, -1), C(6, 5) and D(-7, 6). Show that the mid-points of its sides form a parallelogram.
Question 17 :
PQRS is a rhombus. Its diagonals PR and QS intersect at the point M and satisfy QS = 2PR. If the coordinates of S and M are (1, 1) and (2, -1) respectively, find the coordinates of P.

Answers
1. Answer :
If θ be the angle of inclination of a line with positive direction of x-axis, then the slope of the line is
m = tanθ
Given : θ = 90°.
m = tan90°
m = undefined
2. Answer :
m = tanθ
Given : θ = 0°.
m = tan0°
m = 0
3. Answer :
tanθ = m
Given : m = 1.
tanθ = 1
θ = tan-1(1)
θ = 45°
4. Answer :
tanθ = m
Given : m = 0.
tanθ = 0
θ = tan-1(0)
θ = 0°
5. Answer :
Slope of the line joining (x1, y1) and (x2, y2) is,
m = ⁽ʸ2 ⁻ ʸ1⁾⁄₍ₓ2 ₋ ₓ1₎
Substitute (x1, y1) = (5, 5) and (x2, y2) = (0, 0).
m = ⁽⁰ ⁻ ⁵⁾⁄₍₀ ₋ ₅₎
m = ⁻⁵⁄₋₅
m = 1
6. Answer :
Slope of the line joining (x1, y1) and (x2, y2) :
m = ⁽ʸ2 ⁻ ʸ1⁾⁄₍ₓ2 ₋ ₓ1₎
Substitute
(x1, y1) = (sinθ, -cosθ)
(x2, y2) = (-sinθ, cosθ)
Then, we have
7. Answer :
Mid-point of the segment joining (x1, y1) and (x2, y2) :
Substitute (x1, y1) = (4, 2)- and (x2, y2) = (-6, 4).
= (⁽⁴ ⁻ ⁶⁾⁄₂, ⁽² ⁺ ⁴⁾⁄₂)
= (-²⁄₂, ⁶⁄₂)
= (-1, 3)
Mid-point of the segment joining (4, 2) and (-6, 4) is
P(-1, 3)
Slope of the line joining (x1, y1) and (x2, y2) :
m = ⁽ʸ2 ⁻ ʸ1⁾⁄₍ₓ2 ₋ ₓ1₎
Substitute (x1, y1) = (5, 1) and (x2, y2) = (-1, 3).
m = ⁽³ ⁻ ¹⁾⁄₍₋₁ ₋ ₅₎
m = ²⁄₋₆
m = -⅓
Slope of a line perpendicular to the line joining the points A and P :
8. Answer :
Let A(-3, -4), B(7, 2) and C(12, 5).
Slope of the line joining A(-3, -4) and B(7, 2) :
m = ⁽² ⁺ ⁴⁾⁄₍₇ ₊ ₃₎
m = ⁶⁄₁₀
m = ⅗
Slope of the line joining B(7, 2) and C(12, 5) :
m = ⁽⁵ ⁻ ²⁾⁄₍₁₂ ₋ ₇₎
m = ⅗
Slope of AB and slope of BC are equal and B is a common point.
A, B and C lie on the same line.
Therefore A(-3, -4), B(7, 2) and C(12, 5) are collinear.
9. Answer :
Let A(3, -1), B(a, 3) and C(1, -3).
Slope of the line joining A(3, -1) and B(a, 3) :
m = ⁽³ ⁺ ¹⁾⁄₍ₐ ₋ ₃₎
m = ⁴⁄₍ₐ ₋ ₃₎
Slope of the line joining B(a, 3) and C(1, -3) :
m = ⁽⁻³ ⁻ ³⁾⁄₍₁ ₋ ₐ₎
m = ⁻⁶⁄₍₁ ₋ ₐ₎
Since A(-3, -4), B(7, 2) and C(12, 5) are collinear, slope of AB and slope of BC must be equal.
⁴⁄₍ₐ ₋ ₃₎ = ⁻⁶⁄₍₁ ₋ ₐ₎
4(1 - a) = -6(a - 3)
4 - 4a = -6a + 18
2a = 14
a = 7
10. Answer :
The line through the points (-2, a) and (9, 3) has slope -½. Find the value of a.
Slope of the line joining (-2, a) and (9, 3) :
= ⁽³ ⁻ ᵃ⁾⁄₍₉ ₊ ₂₎
= ⁽³ ⁻ ᵃ⁾⁄₁₁
Given : Slope of the line joining (-2, a) and (9, 3) is -½.
⁽³ ⁻ ᵃ⁾⁄₁₁ = -½
2(3 - a) = -11
6 - 2a = -11
-2a = -17
a = ¹⁷⁄₂
11. Answer :
Slope of the line joining (-2, 6) and (4, 8) :
= ⁽⁸ ⁻ ⁶⁾⁄₍₄ ₊ ₂₎
= ²⁄₆
= ⅓
Slope of the line joining (8, 12) and (x, 24) :
= ⁽²⁴ ⁻ ¹²⁾⁄₍ₓ ₋ ₈₎
= ¹²⁄₍ₓ ₋ ₈₎
Since the lines are perpendicular, the product of the slopes must be equal to -1.
⅓ ⋅ ¹²⁄₍ₓ ₋ ₈₎ = - 1
⁴⁄₍ₓ ₋ ₈₎ = - 1
4 = -(x - 8)
4 = -x + 8
x + 4 = 8
x = 4
12. Answer :
Part (i) :
A(1, -4), B(2, -3) and C(4, -7)
Slope of AB = ⁽⁻³ ⁺ ⁴⁾⁄₍₂ ₋ ₁₎
= ¹⁄₁
= 1
Slope of BC = ⁽⁻⁷ ⁺ ³⁾⁄₍₄ ₋ ₂₎
= -⁴⁄₂
= -2
Slope of AC = ⁽⁻⁷ ⁺ ⁴⁾⁄₍₄ ₋ ₁₎
= -³⁄₃
= -1
Slope of AB x Slope of AC = (-1)(1)
= -1
AB is perpendicular to AC, ∠A = 90°.
Using the distance formula d = √[(x2 - x1)2 + (y2 - y1)2], find the length of each side of the triangle.
Then, Check Pythagorean Theorem for the lengths.
That is, square of the larger side has to be equal to sum of the squares of other two sides.
The vertices are A(1, -4), B(2, -3) and C(4,-7).
AB = √[(x2 - x1)2 + (y2 - y1)2]
Substitute (x1, y1) = (1, -4) and (x2, y2) = (2, -3).
AB = √[(2 - 1)2 + (-3 + 4)2]
= √[12 + 12]
= √[1 + 1]
= √2
AB2 = 2
BC = √[(4 - 2)2 + (-7 + 3)2] = √20
BC2 = 20
AC = √[(4 - 1)2 + (-7 + 4)2] = √18
AC2 = 18
20 = 2 + 18 ----> BC2 = AB2 + AC2
The points A, B and C satisfy Pythagorean theorem.
Therefore, the points A, B and C form a right triangle.
Part (ii) :
L(0, 5), M(9, 12) and N(3, 14).
Slope of LM = ⁽¹² ⁻ ⁵⁾⁄₍₉ ₋ ₀₎
= ⁷⁄₉
Slope of MN = ⁽¹⁴ ⁻ ¹²⁾⁄₍₃ ₋ ₉₎
= ²⁄₋₆
= -⅓
Slope of LN = ⁽¹⁴ ⁻ ⁵⁾⁄₍₃ ₋ ₀₎
= ⁹⁄₃
= 3
Slope of MN x Slope of LN = (-⅓)(3)
= -1
MN is perpendicular to LN, ∠N = 90°.
Using the distance formula d = √[(x2 - x1)2 + (y2 - y1)2], find the length of each side of the triangle.
Then, Check Pythagorean Theorem for the lengths.
That is, square of the larger side has to be equal to sum of the squares of other two sides.
LM = √[(x2 - x1)2 + (y2 - y1)2]
Substitute (x1, y1) = (0, 5) and (x2, y2) = (9, 12).
LM = √[(9 - 0)2 + (12 - 5)2]
= √[92 + 72]
= √[81 + 49]
= √130
LM2 = 130
MN = √[(3 - 9)2 + (14 - 12)2] = √40
MN2 = 40
LN = √[(3 - 0)2 + (14 - 5)2] = √90
LN2 = 90
130 = 40 + 90 ----> LM2 = MN2 + LN2
The points L, M and N satisfy Pythagorean theorem.
Therefore, the points L, M and N form a right triangle.
13. Answer :
In a parallelogram, we can prove that the opposite sides are parallel by showing that the slopes of opposite sides are equal.
A(2.5, 3.5), B(10, -4), C(2.5, -2.5) and D(-5, 5)
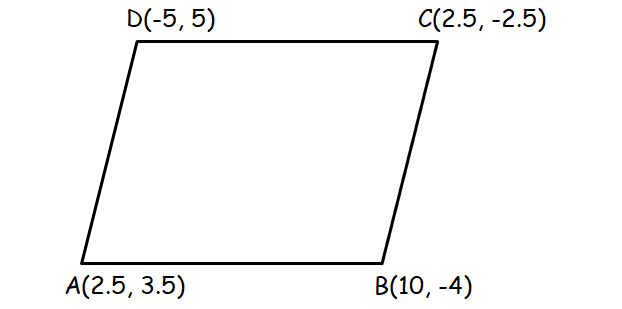
|
Slope of AB : = ⁽⁻⁴ ⁻ ³.⁵⁾⁄₍₁₀ ₋ ₂.₅₎ = -⁷.⁵⁄₇.₅ = -1 Slope of BC : = ⁽⁻².⁵ ⁺ ⁴⁾⁄₍₂.₅ ₋ ₁₀₎ = ¹.⁵⁄₋₇.₅ = -¹⁵⁄₇₅ = -⅕ |
Slope of CD : = ⁽⁵ ⁺ ².⁵⁾⁄₍₋₅ ₋ ₂.₅₎ = -⁷.⁵⁄₇.₅ = -1 Slope of DA : = ⁽⁵ ⁻ ³.⁵⁾⁄₍₋₅ ₋ ₂.₅₎ = ¹.⁵⁄₋₇.₅ = -¹⁵⁄₇₅ = -⅕ |
Slope of AB = Slope of CD
Slope of BC = Slope of DA
Therefore, the given points form a parallelogram.
14. Answer :
Since the given points form a parallelogram,
Slope of AB = Slope of CD
Slope of BC = Slope of DA
A(2, 2), B(–2, –3), C(1, –3) and D(x, y)
|
Slope of AB : = ⁽⁻³ ⁻ ²⁾⁄₍₋₂ ₋ ₂₎ = ⁻⁵⁄₋₄ = ⁵⁄₄ ----(1) |
Slope of CD : = ⁽ʸ ⁺ ³⁾⁄₍ₓ ₋ ₁₎ ----(2) |
|
Slope of BC : = ⁽⁻³ ⁺ ³⁾⁄₍₁ ₊ ₂₎ = ↉ = 0 ----(3) |
Slope of DA : = ⁽ʸ ⁻ ²⁾⁄₍ₓ ₋ ₂₎ ----(4) |
(1) = (2) :
⁵⁄₄ = ⁽ʸ ⁺ ³⁾⁄₍ₓ ₋ ₁₎
5(x - 1) = 4(y + 3)
5x - 5 = 4y + 12
5x - 4y = 12 + 5
5x - 4y = 17 -----(5)
(3) = (4) :
0 = ⁽ʸ ⁻ ²⁾⁄₍ₓ ₋ ₂₎
0 = y - 2
2 = y
Substitute y = 2 into (5).
5x - 4(2) = 17
5x - 8 = 17
5x = 25
x = 5
Therefore,
(x, y) = (5, 2)
15. Answer :
A(3, -4), B(9, -4) , C(5, -7) and D(7, -7)
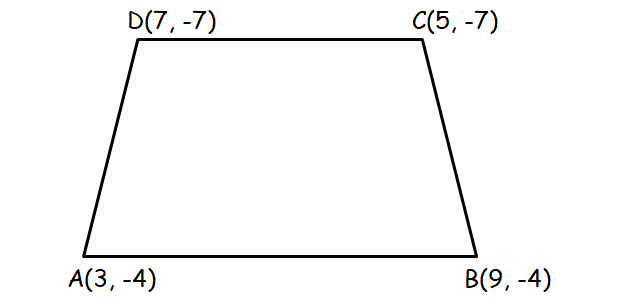
A trapezium always contains two parallel sides and two non parallel sides.
Slope of AB = (-4 + 4)/(9 - 3)
= 0/6
= 0
Slope of BC = (-7 + 4)/(5 - 9)
= -3/-4
= 3/4
Slope of CD = (-7 + 7)/(7 - 5)
= 0/2
= 0
Slope of DA = (-7 + 4)/(7 - 3)
= -3/4
From the above working, we have
Slope of AB = Slope of CD ----> AB and CD are parallel
Slope of BC ≠ Slope of DA ----> BC and DA are not parallel
Therefore, ABCD is a trapezium.
16. Answer :
A(-4, -2), B(5, -1), C(6, 5) and D(-7, 6)
Lep P, Q, R and S be the mid-points of the sides AB, BC, CD and DA respectively.
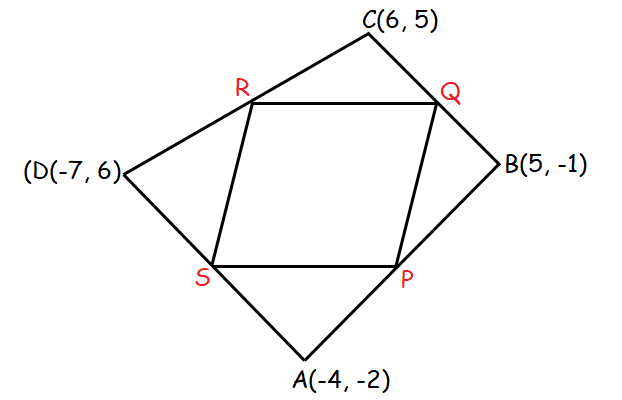
Midpoint of the side AB :
= P(⁽⁻⁴ ⁺ ⁵⁾⁄₂, ⁽⁻² ⁻ ¹⁾⁄₂)
= P (½, -³⁄₂)
Midpoint of the side BC :
= Q(⁽⁵ ⁺ ⁶⁾⁄₂, ⁽⁻¹ ⁺ ⁵⁾⁄₂)
= Q(¹¹⁄₂, ⁴⁄₂)
= Q(¹¹⁄₂, 2)
Midpoint of the side CD :
= R(⁽⁻⁷ ⁺ ⁶⁾⁄₂, ⁽⁶ ⁺ ⁵⁾⁄₂)
= R(-¹⁄₂, ¹¹⁄₂)
Midpoint of the side DA :
= S(⁽⁻⁷ ⁻ ⁴⁾⁄₂, ⁽⁻² ⁺ ⁶⁾⁄₂)
= S(-¹¹⁄₂, ⁴⁄₂)
= S(-¹¹⁄₂, 2)
Slope of SR :
Slope of PQ :
Slope of PQ = Slope of SR
Slope of SP :
Slope of RQ :
Slope of SP = Slope of RQ
17. Answer :
Let (a, b) be the coordinates of P.
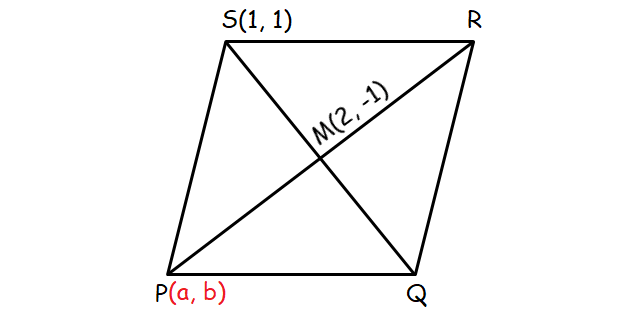
Slope of SQ (use the coordinates of S and M) :
= ⁽⁻¹ ⁻ ¹⁾⁄₍₂ ₋ ₁₎
= ⁻²⁄₁
= -2
Slope of PR (use the coordinates of P and M) :
= ⁽⁻¹ ⁻ ᵇ⁾⁄₍₂ ₋ ₐ₎
In a rhombus, always diagonals are perpendicular.
So, the product of the slopes of the disgonals SQ and PS is equal to -1.
-2 ⋅ ⁽⁻¹ ⁻ ᵇ⁾⁄₍₂ ₋ ₐ₎ = -1
⁽² ⁺ ²ᵇ⁾⁄₍₂ ₋ ₐ₎ = -1
2 + 2b = -1(2 - a)
2 + 2b = -2 + a
2b + 4 = a
a = 2b + 4 ----(1)
Distance between S(1, 1) and M(2, -1) :
SM = √[(x2 - x1)2 + (y2 - y1)2]
SM = √[(2 - 1)2 + (-1 - 1)2]
SM = √[12 + (-2)2]
SM = √(1 + 4)
SM = √5
In a rhombus, always diagonals bisect each other. So, M is the midpoint of QS and PR.
QS = 2(SM)
QS = 2√5
Given : QS = 2PR.
2PR = 2√5
PR = √5
2(PM) = √5
Squaring both sides,
Substitute a = 2b + 4.
4(4b2 + 8b + 4 + 1 + 2b + b2) = 5
4(5b2 + 10b + 5) = 5
4 ⋅ 5(b2 + 2b + 1) = 5
Divide both sides by 5.
4(b2 + 2b + 1) = 1
4(b + 1)2 = 1
(b + 1)2 = ¼
b + 1 = ±√¼
b + 1 = ±√¼
|
b + 1 = ½ b = ½ - 1 b = -½ Substitute b = -½ in (1). a = 2(-½) + 4 a = -1 + 4 a = 3 |
b + 1 = -½ b = -½ - 1 b = -³⁄₂ Substitute b = -³⁄₂ in (1). a = 2(-³⁄₂) + 4 a = -3 + 4 a = 1 |
(a, b) = (3, -½) or (1, -³⁄₂)
The coordinates of P are (3, -½) or (1, -³⁄₂).
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
