PROVING TRIANGLES ARE SIMILAR

In this section, you will study the three ways to prove that two triangles are similar. 

1. Side-Side-Side (SSS) Similarity Theorem

2. Side-Angle-Side (SAS) Similarity Theorem

3. Angle-Angle (AA) Similarity Postulate. 

Side-Side-Side (SSS) Similarity Theorem

If the lengths of the corresponding sides of two triangles are proportional, then the triangles are similar.

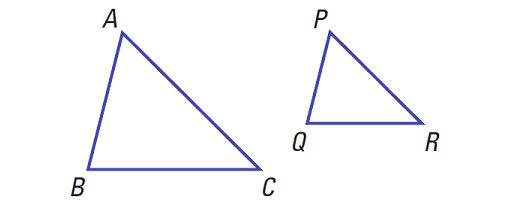
In the diagram above, 

if AB/PQ  =  BC/QR  =  CA  =  RP, then 

ΔABC  ∼  ΔPQR

Side-Angle-Side (SAS) Similarity Theorem

If an angle of one triangle is congruent to an angle of a second triangle and the lengths of the sides including these angles are proportional, then the triangles are similar.

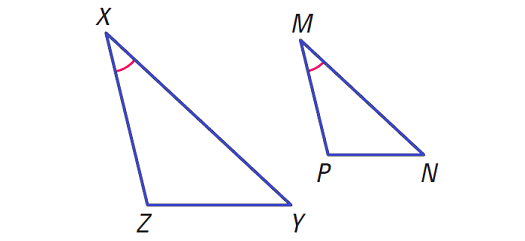
In the diagram above, 

if ∠X  ≅  ∠M and ZX/PM  =  XY/MN, then

ΔXYZ  ∼  ΔMNP

Angle-Angle(AA) Similarity Postulate

If two angles of one triangle are congruent to two angles of another triangle, then the two triangles are similar.

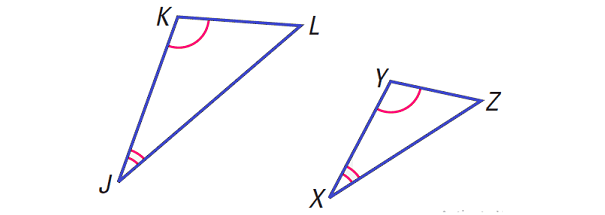
In the diagram above, 

if ∠JKL  ≅  ∠XYZ and ∠KJL  ≅  ∠YXZ, then

ΔJKL  ∼  ΔXYZ

Proof of Side-Side-Side (SSS) Similarity Theorem

In the triangles LMN and RST,  

RS/LM  =  ST/MN  =  TR/NL

Prove : ΔRST  ∼  ΔLMN

Solution :

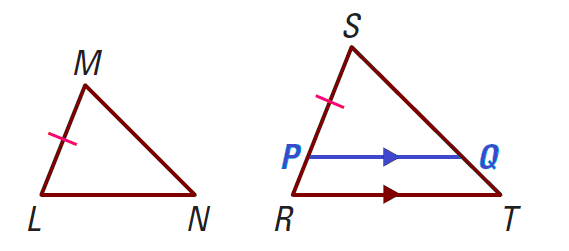
Locate P on RS so that PS  =  LM.

Draw PQ so that PQ ∥ RT.

Then ΔRST  ∼ ΔPSQ, by the Angle Angle (AA) Similarity Postulate, and 

RS/PS  =  ST/SQ  =  TR/QP

Because PS = LM, we can substitute in the given proportion and find that SQ  =  MN and QP  =  NL. 

By the SSS Congruence Theorem, it follows that

ΔPSQ  ≅  ΔLMN

Finally, use the definition of congruent triangles and the AA Similarity Postulate to conclude that

ΔRST  ∼  ΔLMN

Using the SSS Similarity Theorem

Example 1 :

Which of the following three triangles are similar ?

Solution :

To decide which, if any, of the triangles are similar, we need to consider the ratios of the lengths of corresponding sides.

Ratios of Side Lengths of ΔABC and ΔDEF : 

AB/DE  =  6/4  =  3/2

CA/FD  =  12/8  =  3/2

BC/EF  =  9/6  =  3/2

Because all of the ratios are equal, ΔABC ∼ ΔDEF.

Ratios of Side Lengths of ΔABC and ΔGHJ : 

AB/GH  =  6/6  =  1

CA/JG  =  12/14  =  6/7

BC/HJ  =  9/10

Because the ratios are not equal, ΔABC and ΔGHJ are not similar.

Since ΔABC is similar to ΔDEF and ΔABC is not similar to ΔGHJ, ΔDEF is not similar to ΔGHJ.

Using the SAS Similarity Theorem

Example 2 :

In the diagram shown below, use the given lengths to prove that ΔRST ∼ ΔPSQ. 

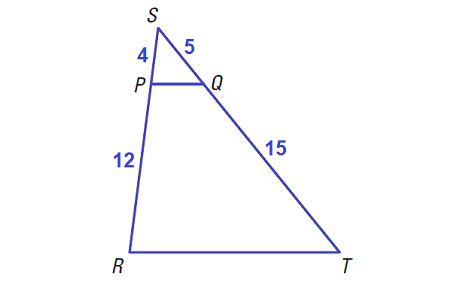
Solution :

Given : SP = 4, PR = 12, SQ = 5, QT = 15

Prove : ΔRST ∼ ΔPSQ

Use the SAS Similarity Theorem.

Begin by finding the ratios of the lengths of the corresponding sides.

SR/SP  =  (SP + PR)/SP  =  (4 + 12)/4  =  16/4  =  4

ST/SQ  =  (SQ + QT)/SQ  =  (5 + 15)/5  =  20/5  =  4

So, the lengths of sides SR and ST are proportional to the lengths of the corresponding sides of ΔPSQ.

Because ∠S is included angle in both triangles, use the SAS Similarity Theorem to conclude that 

ΔRST  ∼  ΔPSQ

Using the AA Similarity Postulate

Example 3 :

Determine whether the two triangles shown below are similar. Justify your answer.

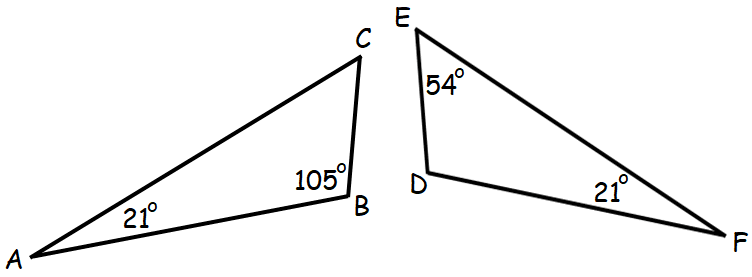
Solution :

By Triangle Sum Theorem, in Δ ABC,

∠A + ∠B + ∠C  =  180°

21° + 105° + ∠C  =  180°

126° + ∠C  =  180°

Subtract 126° from both sides.

∠C  =  54°

In triangles ABC and DEF, we have

∠A  =  ∠F  =  21°

∠E  =  ∠C  =  54°

Two angles of one triangle are congruent to two angles of another triangle.

By Angle-Angle (AA) Similarity Postulate, the triangles ABC and DEF are similar triangles.  

Using Similar Triangles in Real Life

Example (Using a Pantograph) :

As we move the tracing pin of a pantograph along a figure, the pencil attached to the far end draws an enlargement. As the pantograph expands and contracts, the three brads and the tracing pin always form the vertices of a parallelogram. The ratio of PR to PT is always equal to the ratio of PQ to PS. Also, the suction cup, the tracing pin, and the pencil remain collinear.

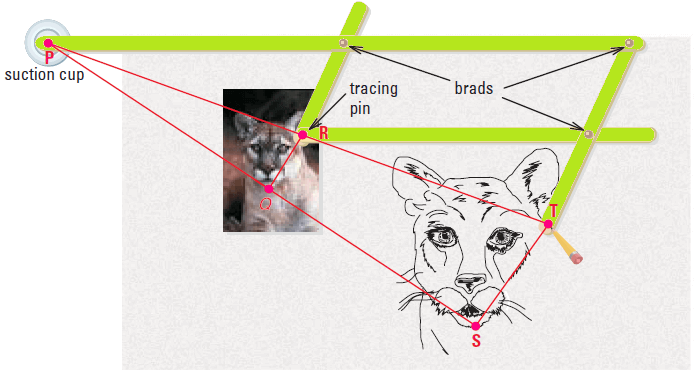
a. How can we prove that ΔPRQ  ∼  ΔPTS ?

b. In the diagram, PR is 10 inches and RT is 10 inches. The length of the cat RQ, in the original print is 2.4 inches. Find the length TS in the enlargement.

Solution (a) :

We know that PR/PT  =  PQ/PS. 

Because ∠P  ≅  ∠P, we can apply the SAS Similarity Theorem to conclude that 

ΔPRQ  ∼  ΔPTS

Solution (b) :

Because the triangles are similar, we can set up a proportion to find the length of the cat in the enlarged drawing.

Write proportion :

PR/PT  =  RQ/TS

Substitute. 

10/20  =  2.4/TS

Solve for TS.

TS  =  4.8

Hence, the length of the cat in the enlarged drawing is 4.8 inches. 

Finding Distance Indirectly

Example (Indirect Measurement) :

To measure the width of a river, we use a surveying technique, as shown in the diagram. Use the given lengths (measured in feet) to find RQ.

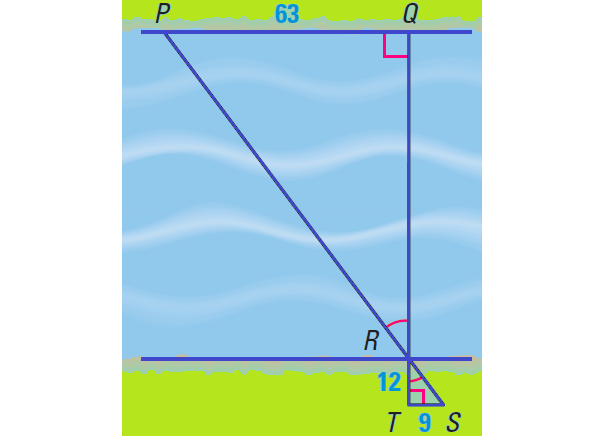
Solution :

By the AA Similarity Postulate, 

ΔPQR  ∼  ΔSTR

Write proportion. 

RQ/RT  =  PQ/ST

Substitute.

RQ/12  =  63/9

Simplify. 

RQ/12  =  7

Multiply each side by 12. 

12 ⋅ (RQ/12)  =  7 ⋅ 12

RQ  =  84

So, the river is 84 feet wide.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.