PROVING TRIGONOMETRIC IDENTITIES SAMPLE PROBLEMS

Problem 1 :

If (cos⁴α/cos²β) + (sin⁴α/sin²β)  =  1, prove that

(i) sin⁴α + sin⁴β  =  2sin²αsin²β

(ii) (cos⁴β/cos²α) + (sin⁴β/sin²α)  =  1

Solution :

Given that :

(cos⁴α/cos²β) + (sin⁴α/sin²β)  =  1

((cos⁴α sin²β + sin⁴α cos²β) / cos²β sin²β)  =  1

((cos⁴α sin²β + sin⁴α cos²β) / cos²β sin²β)  =  1

cos⁴α sin²β + sin⁴α cos²β  =  cos²β sin²β

cos⁴α (1- cos²β) + cos²β (1 - cos²α)²  =  cos²β sin²β

cos⁴α (1- cos²β) + cos²β(1 + cos⁴α - 2cos²α) = cos²β sin²β

cos⁴α - cos⁴α cos²β + cos²β + cos²β cos⁴α - 2cos²β cos²α 

=  cos²β(1 - cos²β)

cos⁴α - cos⁴α cos²β + cos²β + cos²β cos⁴α - 2cos²β cos²α  - cos²β + cos⁴β  =  0

cos⁴α - 2cos²β cos²α + cos⁴β  =  0

(cos²α - cos²β)²  =  0

cos²α  =  cos²β

1 - sin²α  =  1 - sin²β

sin²α  =  sin²β

(i)  sin⁴α + sin⁴β  =  2sin²α sin²β

L.H.S :

  =  sin⁴α + sin⁴β

  =  (sin²α - sin²β)² + 2sin²α sin²β

  =  (sin² α - sin² α)² + 2sin² α sin² β

  =  2sin²α sin²β  ----> R.H.S

(ii) (cos⁴β/cos²α) + (sin⁴β/sin²α)  =  1.

  =  (cos² β cos² β/cos²α) + (sin²β sin²β/sin²α)

  =  (cos²β cos²α/cos²α) + (sin²β sin²α/sin²α)

  =  cos²β + sin²β

  =  1

= R.H.S

Problem 2 :

If y = 2 sinα/(1 + cosα + sinα), then prove that

(1 − cosα + sinα)/(1 + sinα)  =  y

Solution :

(1 − cos α + sin α)/(1 + sin α)

Multiply both numerator and denominator by (1 + cosα + sinα).

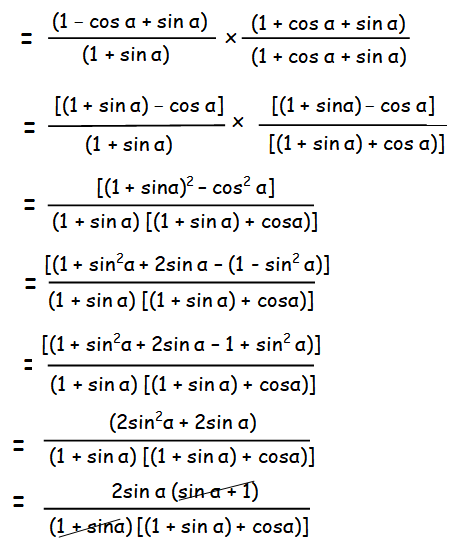
=   2sinα/(1 + cosα + sinα)

Hence proved.

Problem 3 :

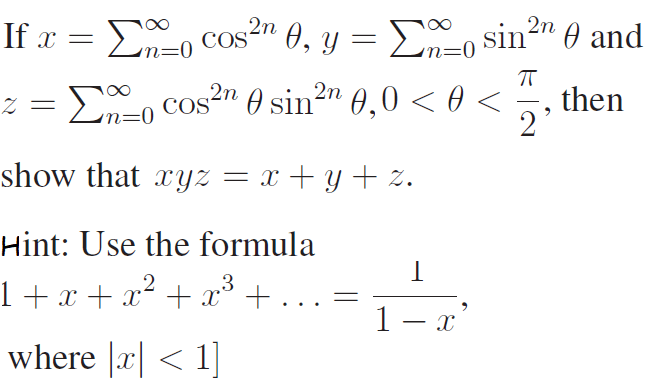
Solution :

x  = 1 + cos²θ + cos⁴θ + cos⁶θ + .............

x  =  1 / (1 - cos²θ)  =  1/sin²θ 

y  = 1 + sin²θ + sin⁴θ + sin⁶θ + .............

y  =  1 / (1 - sin²θ)  =  1/cos²θ

y  = 1 + cos²θ sin²θ + cos⁴θ sin⁴θ +  .............

z  =  1 / (1 - sin²θ cos²θ)  =  1/(1 - sin²θcos²θ)

L.H.S 

xyz  =  (1/sin²θ) (1/cos²θ) (1/(1 - sin²θ cos²θ))

=  1/[sin²θ cos²θ(1 - sin²θ cos²θ)]

R.H.S

x + y + z  =  (1/sin²θ) + (1/cos²θ) + (1/(1 - sin²θ cos²θ)) 

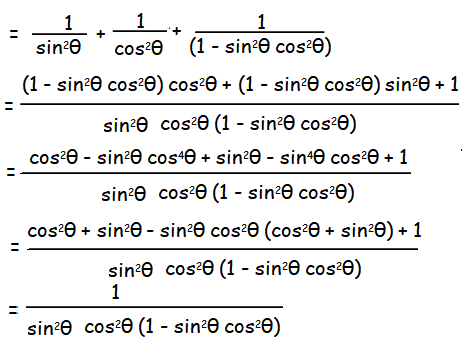
Hence proved.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.