PSAT MATH QUESTIONS

Question 1 :

If x*  =  7/x, what is the value of 14 (14*) ?

Solution :

Given : x*  =  7/x. 

Then, we have

14(14*)  =  14(7/14)

  14(14*)  =  14(1/2)

14(14*)  =  7

Hence, the answer is 7.

Question 2 :

What is the least common multiple of 4, 16, 25, and 30 ?

Solution :

least common multiple  =  2 ⋅ 2 ⋅ 5 ⋅ 4 ⋅ 5 ⋅ 3

  =  1200

Question 3 :

How many positive integers are between -7/3 and 5/2 ?

Solution :

The decimal form of -7/3  =  -2.33

Decimal form of 5/2  =  2.5

Between -7/3 and 5/2, we have 

-2, -1, 0, 1, 2

Integers are 1 and 2.

Hence there are 2 positive integers between -7/3 and 2/5.

Question 4 :

The perimeter of the rectangle is 80 inches. If the width is 18 inches, what is the area of the rectangle ?

Solution :

Perimeter of rectangle  =  80 inches

2 (l + w)  =  80

l + w  =  40

width  =  18 inches

l + 18  =  40

l  =  40 - 18  =  22 inches

Area of the rectangle is 

=  l ⋅ w

=  22 ⋅ 18

=  396 square inches.

Question 5 :

7|-x - 3|  =  b, if x = -3, what is b ?

Solution :

7|-x - 3|  =  b

Substitute -3 for x. 

7|-(-3) - 3|  =  b

7|3 - 3|  =  b

7|0|  =  b

0  =  b

So, the value of b is 0.

Question 6 :

1 + 2 + 3 + 4 + 5 + ............. + 100  =  

Solution :

To find the sum of first n natural numbers, we have a formula

S_n  =  n(n + 1)/2

S₁₀₀  =  100(100 + 1)/2

  =  50 (101)

=  5050

Hence the answer is 5050.

Question 7 :

After a 10% increase, a population was 55. What was the population before the increase ?

Solution :

Let "x" be the population before the increase.

x + 10% of x  =  55

x + 10x/100  =  55

 x + x/10  =  55

(10x + x) /10  =  55

11x/10  =  55

x  =  55 (10/11)

x  =  50

Question 8 :

The length of a rectangular solid is 10. The width, w and the height h follow the relationship, w³h³  =  27. What is the volume of the rectangular solid ?

Solution :

w³h³  =  27

(wh)³  =  27

(wh)³  =  3³ ==> wh  =  3

Length of rectangular solid  =  10

Volume of rectangular solid  =  lwh

=  10 (3)

=  30

Question 9 :

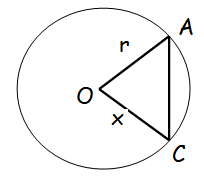
AC has a length of 10 and r, the radius is 7. What is x ?

Solution :

OA  =  r (radius)

OC  =  x (radius)

Hence the value of x is 7.

Question 10 :

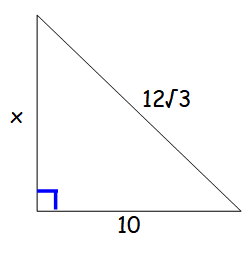
Find the value of x in the diagram shown above.  

Solution :

In a right triangle, the square of hypotenuse side is equal to the sum of squares of other two sides.

(12√3)²   =  x² + 10² 

144(3)  =  x² + 100

x²  =  432 - 100  =  332

x  =  √332

Question 11 :

A contract for a certain service requires a onetime activation cost of $35 and a monthly cost of $23. Which equation represents this situation, where c is the total cost, in dollars, of this service contract for t months?

A)  c = (t/23) + 35     B)  c = (t/35) + 23

C)  c = 23t + 35     D)  c = 35t + 23

Solution :

Onetime activation cost = $35

Number of months = t

Monthly cost = $23

Total cost = c

c = 23t + 35

So, option C is correct.

Question 12 :

x = 4

y = 5 − x

The solution to the given system of equations is (x, y). What is the value of y ?

A) 1       B) 4     C) 5       D) 9

Solution :

x = 4 ----(1)

y = 5 − x -----(2)

Applying x = 4 in (2), we get

y = 5 - 4

y = 1

So, the value of y is 1. Option A is correct.

Question 13 :

The function f is defined by f (x) = 3x −8. What is the value of f (7) ?

A) 29    B) 13     C) −5        D) −29

Solution :

f(x) = 3x − 8

To find f(7), we have to apply 7 in the place of x in the given function.

f(7) = 3(7) - 8

= 21 - 8

= 13

So, the value of f(7) is 13. Option B is correct.

Question 14 :

Each of 157 gemstones can be classified as one of three classifications, as shown in the frequency table.

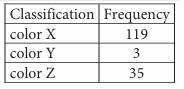
If one of the gemstones is selected at random, what is the probability of selecting a gemstone of color Y?

A) 3/157     B) 35/157    C) 119/157    D) 154/157

Solution :

Total number of gemstones = 157

Number of gemstones of color Y = 3

Probability of selecting color Y = 3/157

So, option A is correct.

Question 15 :

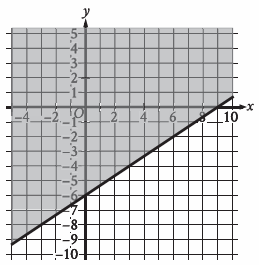
The shaded region shown represents the solutions to which inequality?

A)  y ≥ (2/3)x - 6          B)  y ≥ (2/3)x + 6

C)  y ≥ (2/3)x - 9          D)  y ≥ (2/3)x + 9

Solution :

Finding equation of line shown above :

y-intercept = -6

(6, -2)  and (9, 0)

Slope = (y₂ - y₁)/(x₂ - x₁)

= (0 - (-2)) / (9 - 6)

= (0 + 2) / 3

= 2/3

y = (2/3) x - 6

Let us select one of the points above the line and apply in the equation we have created. So, based on the condition we get we can choose the inequality sign required.

(4, 0)

0 = (2/3) (4) - 6

0 = 8/3 - 6

0 = -10/3

To make this statement true, we have to use ≥ sign. So, the answer is 

y ≥ (2/3)x - 6

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.