PYTHAGOREAN THEOREM IN THREE DIMENSIONS
The Pythagorean Theorem
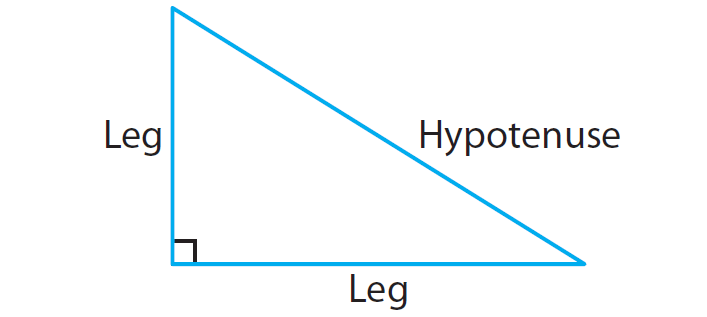
In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.
If a and b are legs and c is the hypotenuse, then
a2 + b2 = c2
Example 1 :
A box used for shipping narrow silver sticks measures 6 inches by 6 inches by 20 inches. What is the length of the longest stick that will fit in the box, given that the length of the tube must be a whole number of inches ?
Solution :
Step 1 :
Draw an appropriate diagram for the given information.
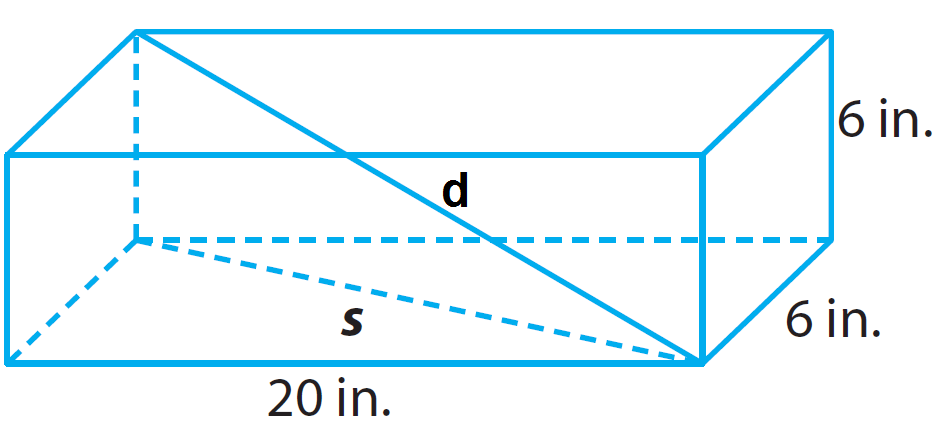
From the diagram given above, the box has the following dimensions.
Length (l) = 20 in.
Width (w) = 6 in.
Height (h) = 6 in.
Step 2 :
We want to find d, the length from a bottom corner to the opposite top corner. First, find s, the length of the diagonal across the bottom of the box.
w2 + l2 = s2
Step 3 :
Substitute the given measures.
62 + 202 = s2
Simplify.
36 + 400 = s2
436 = s2
Step 3 :
Use the expression for s to find d.
h2 + s2 = d2
Step 4 :
Plug h = 6 and s2 = 436.
62 + 436 = d2
Simplify.
36 + 436 = d2
472 = d2
Take square root on both sides.
√472 = √d2
21.7 ≈ d
Hence, the length of the longest stick that will fit in the box is 21 inches.
Example 2 :
Lily ordered a replacement part for her desk. It was shipped in a box that measures 4 in. by 4 in. by 14 in. What is the greatest length in whole inches that the part could have been ?
Solution :
Step 1 :
Draw an appropriate diagram for the given information.
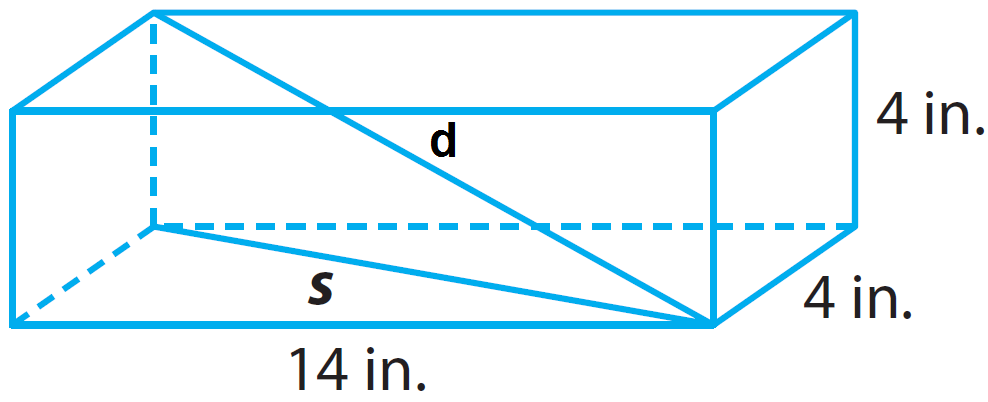
From the diagram given above, the box has the following dimensions.
Length (l) = 14 in.
Width (w) = 4 in.
Height (h) = 4 in.
Step 2 :
We want to find d, the length from a bottom corner to the opposite top corner. First, find s, the length of the diagonal across the bottom of the box.
w2 + l2 = s2
Step 3 :
Substitute the given measures.
42 + 142 = s2
Simplify.
16 + 196 = s2
212 = s2
Step 3 :
Use the expression for s to find d.
h2 + s2 = d2
Step 4 :
Plug h = 4 and s2 = 212.
42 + 212 = d2
Simplify.
16 + 212 = d2
228 = d2
Take square root on both sides.
√228 = √d2
15.1 ≈ d
Hence, the greatest length that the part could have been 15 inches.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
De Moivre's Theorem and Its Applications
Apr 19, 24 08:30 AM
De Moivre's Theorem and Its Applications -
First Fundamental Theorem of Calculus - Part 1
Apr 17, 24 11:27 PM
First Fundamental Theorem of Calculus - Part 1 -
Polar Form of a Complex Number
Apr 16, 24 09:28 AM
Polar Form of a Complex Number
