QUADRILATERAL EXAMPLE PROBLEMS WITH FOUR VERTICES

Question 1 :

If vertices of quadrilateral are at A(-5, 7) , B(-4, k) , C(-1, -6) and D(4, 5) and its area is 72 sq.units. Find the value of k.

Solution :

Area of quadrilateral  =  72 sq.units

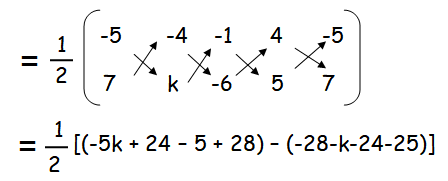
(-5k + 52 - 5) - (-77 - k)  =  2(72)

-5k + 47 + 77 + k  =  144

-4k + 124  =  144

-4k  =  144 - 124

-4k  =  20

k  =  -5

Question 2 :

Without using distance formula, show that points (-2, -1) , (4, 0) , (3, 3) and (-3, 2) are the vertices of a parallelogram.

Solution :

Let the given vertices be A (-2, -1) B (4, 0) C (3, 3) and D (-3, 2).

If the given vertices form a parallelogram,

Midpoint of AC  =  Midpoint of BD

Midpoint  =  (x₁ + x₂)/2, (y₁ + y₂)/2

Midpoint of AC  =  (-2 + 3)/2, (-1 + 3)/2

  =  (1/2, 2/2)

  =  (1/2, 1)-------(1)

Midpoint of BD  =  (4 + (-3))/2, (0 + 2)/2

  =  (1/2, 2/2)

  =  (1/2, 1)-------(2)

Hence the given points form a parallelogram.

Question 3 :

Find the equations of the lines, whose sum and product of intercepts are 1 and –6 respectively.

Solution :

Let "a" and "b" be the x and y -intercepts.

Sum of intercept  =  1

a + b  =  1

Product of intercept  =  -6

ab  =  -6

b  =  -6/a

a + (- 6/a)  =  1

a² - 6  =  a

a² - a - 6  =  0

(a - 3) (a + 2)  =  0

a  =  3 and a = -2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.