QUESTIONS BASED ON ANGLE OF ELEVATION

To find the questions 1 and 2, please visit the page "Angle of Elevation Practice Problems".

Question 3 :

To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? (√3 = 1.732)

Solution :

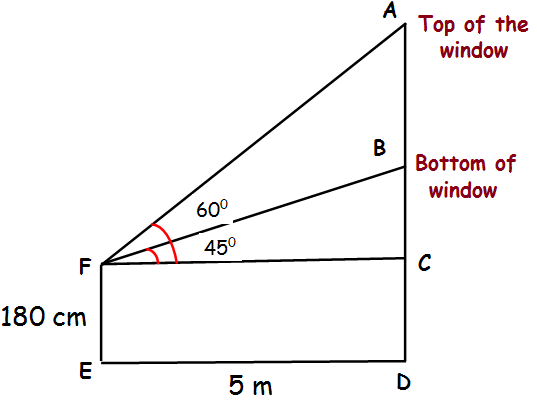
Height of window  =  AB

180 cm  =  1.8 m

In triangle FBC,

tan θ  =  Opposite side / Adjacent side 

tan 45  =  BC/FC

1  =  BC/5

BC  =  5 m

In triangle FBC,

tan 60  =  AC/FC

√3  =  AC/5

AC  =  5√3

AB  =  AC - BC

  =  5√3 - 5

  =  5(√3 - 1)

  =  5(1.732 - 1)

  =  5(0.732)

  =  3.66 m 

Hence height of window is 3.66 m.

Question 4 :

A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 40° . Find the height of the pedestal. (tan 40° = 0.8391, √3 = 1.732)

Solution :

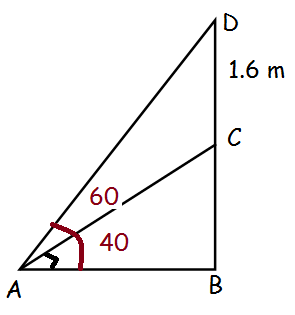
In triangle ABC, 

tan θ  =  Opposite side / Adjacent side 

tan 40  =  BC/AB

0.8391  =  BC/AB

Let BC = x

0.8391  =  x/AB

AB  =  x/0.8391  -----(1)

In triangle ABD,

tan 60  =  BD/AB

√3  =  (1.6 + x)/AB

AB  =  (1.6 + x)/√3 -----(2)

(1)  =  (2)

x/0.8391  =  (1.6 + x)/√3

√3x  =  (1.6 + x) 0.8391

1.732x - 0.8391x  =  1.6(0.8391)

 0.8929x  =  1.34256

x  =  1.34256/0.8929

x  =  134256/89290

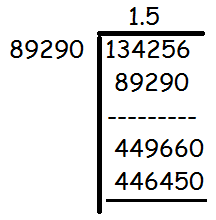
Hence the height of the pedestal is 1.5 m.

Question 5 :

A flag pole ‘h’ meters is on the top of the hemispherical dome of radius ‘r’ meters. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30° . Find (i) the height of the pole (ii) radius of the dome. (√3 = 1.732)

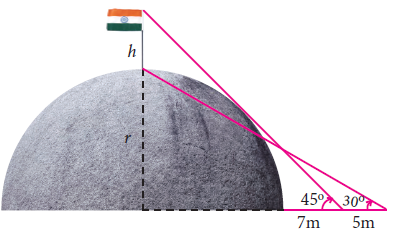
Solution :

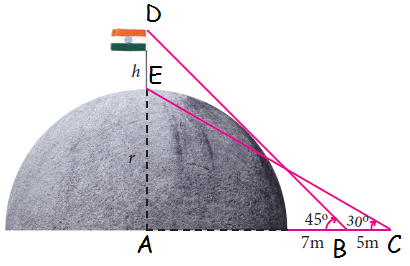
In triangle ADB, 

tan θ  =  Opposite side / Adjacent side 

tan 45  =  (r + h)/AB

1  =  (r + h)/(r + 7)

r + h = r + 7

r - r + h =  7

h = 7 m

In triangle ADC,

tan 30  =  AE/AC

1/√3  =  r / (r + 12)

r + 12  =  √3r

r(1 - √3)  =  -12

r = [12/(√3 - 1)]  [(√3 + 1)/(√3 + 1)]

  =  12(√3 + 1)/2

  =  6(1.732 + 1)

  =  6(2.732)

r  =  16.39 m

(i) the height of the pole = 7m

(ii) radius of the dome  =  16.39 m

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.