QUESTIONS ON BINOMIAL EXPANSION INCLUDING EXPONENTIAL FUNCTIONS AND LOGARITHMIC FUNCTIONS

(1)  Expand the following in ascending powers of x and find the condition on x for which the binomial expansion is valid. 

(i)  1/(5 + x)            Solution

(ii)  2/(3 + 4x)²         Solution

(iii)  (5 + x²)^2/3           Solution

(iv)  (x + 2)^-2/3            Solution

(2)  Find ³√1001 approximately (two decimal places).

Solution

(3)  Prove that ³√(x³ + 6) − ³√(x³ + 3) is approximately equal to 1/x² when x is sufficiently large.  Solution

(4)  Prove that √(1−x)/(1+x) is approximately equal to 1 − x + x² when x is very small.     Solution

(5)  Write the first 6 terms of the exponential series

(i) e^5x                 Solution

(ii)  e^−2x             Solution

(iii)  e^(1/2)x             Solution

(6)  Write the first 4 terms of the logarithmic series

(i)  log (1 + 4x)           Solution

(ii)  log(1 − 2x)          Solution

(iii)  log [(1+3x)/(1−3x)]            Solution

(iv)  log [(1-2x)/(1+2x)]          Solution

(7)  If y = x + x²/2 + x³/3 + x⁴/4 + · · · , then show that x = y − y²/2! + y³/3! − y⁴/4! + · · · .            Solution

(8)  If p − q is small compared to either p or q, then show that

Solution

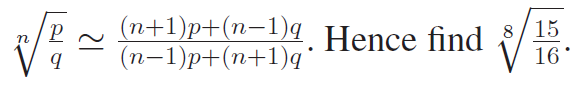
(9)  Find the coefficient of x⁴ in the expansion of (3−4x+x²)/e^2x .             Solution

(10)  Find the value of 

Solution

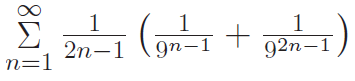
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.