QUESTIONS ON CUBE ROOT OF UNITY FOR CLASS 12

Question 1 :

Find the cube root of unity.

Solution :

Let z = (1)^1/3

Writing 1 in polar form

1 = cos 0 + i sin 0

(1)^1/3 = [cos (0 + 2kπ) + i sin (0 + 2kπ)]^1/3

(1)^1/3 = [cos 2kπ + i sin 2kπ]^1/3

= [cos 2kπ/3 + i sin 2kπ/3]

Applying k = 0

= [cos 0 + i sin 0]

= 1

Applying k = 1

= [cos 2kπ/3 + i sin 2kπ/3]

= cos (2π/3) + i sin (2π/3)

cos (2π/3) = -1/2

sin (2π/3) = √3/2

cos (2π/3) + i sin (2π/3) = -1/2 + i(√3/2)

Applying k = 2

= [cos 2kπ/3 + i sin 2kπ/3]

= cos (4π/3) + i sin (4π/3)

cos (4π/3) = 1/2

sin (4π/3) = -√3/2

cos (4π/3) + i sin (4π/3) = 1/2 - i(√3/2)

So, cube root of unity are

1, -1/2 + i(√3/2) and 1/2 - i(√3/2)

Question 2 :

Solve the equation z³ + 8i = 0

Solution :

z³ + 8i = 0

z³ = - 8i

z = (-8i)^1/3

z = (-8)^1/3i^1/3

z = -2 i^1/3

Writing 1 in polar form

1 = cos 0 + i sin 0

-2 (1)^1/3 = -2 [cos (0 + 2kπ) + i sin (0 + 2kπ)]^1/3

-2 (1)^1/3 = -2 [cos 2kπ + i sin 2kπ]^1/3

= -2 [cos 2kπ/3 + i sin 2kπ/3]

Applying k = 0

= -2 [cos 0 + i sin 0]

= -2

Applying k = 1

= -2 [cos 2kπ/3 + i sin 2kπ/3]

= -2 [cos (2π/3) + i sin (2π/3)]

cos (2π/3) = -1/2

sin (2π/3) = √3/2

-2 [cos (2π/3) + i sin (2π/3)] = -2[-1/2 + i(√3/2)]

= 1 - i√3

Applying k = 2

=-2[cos 2kπ/3 + i sin 2kπ/3]

= -2[cos (4π/3) + i sin (4π/3)]

cos (4π/3) = 1/2

sin (4π/3) = -√3/2

-2 [cos (4π/3) + i sin (4π/3)] = -2[1/2 - i(√3/2)]

= -1 + i√3

So, the required roots are 

1, 1 - i√3 and -1 + i√3

Question 3 :

If ω ≠ 1 is a cube root of unity, show that

[(a + b ω + cω²)/(b + c ω + a ω²)] + [(a + b ω + cω²)/(c + a ω + b ω²)]  =  -1

Solution :

L.H.S :

Multiply both numerator and denominator of the first fraction by ω²

  =   (ω²/ω²) [(a + b ω + cω²)/(b + c ω + a ω²)]

  =  [ω²(a + b ω + cω²)/ω²(b + c ω + a ω²)]

  =  (aω^{2 +} b ω³ + cω⁴)/ω²(b + c ω + a ω²)

  =  (aω^{2 +} b + cω)/ω²(b + c ω + a ω²)

  =  1/ω²  ----(1)

Multiply both numerator and denominator of the second fraction by ω

  =  (ω/ω) [(a + b ω + cω²)/(c + a ω + b ω²)]

  =  [ω(a + b ω + cω²)/ω(c + a ω + b ω²)]

=  (aω + bω² + cω³)/ω(c + a ω + b ω²)

=  (c + a ω + b ω²)/ω(c + a ω + b ω²)

=  1/ω----(2)

(1) + (2)

  =   (1/ω²) + (1/ω)

  =  (ω + ω²)/ω³

  =  -1/1

  =  -1  R.H.S

Hence proved.

Question 4 :

Show that 

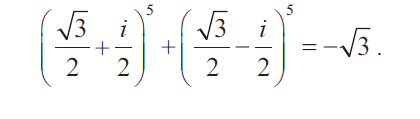
Solution :

First let us try to write the given complex numbers in polar form.

[(√3 + i)/2]⁵

r  =  √[(√3/2)² + (1/2)²]

r  =  √[(3 + 1)/4]

r  =   1

Argument :

α  = tan^-1|y/x|

α  = tan^-1|(1/2) / (√3/2)|

  =  tan^-1|(1/√3)|

α  = π/6

Polar form of the first part,

 [(√3 + i)/2]⁵  =  1(cosπ/6 + i sin π/6)⁵

By applying De moiver's theorem, we get

=  (cos 5π/6 + i sin 5π/6)  -----(1)

Similarly, polar form of the second part

 [(√3 - i)/2]⁵  =  1(cosπ/6 - i sin π/6)⁵

By applying De moiver's theorem, we get

=  (cos 5π/6 - i sin 5π/6)  -----(2)

(1) + (2)

  =  2 cos 5π/6

  =  2 cos (150)

  =  2 cos (180 - 30) (lies in 2^nd quadrant)

  =  -2 (√3/2)

  =  - √3 

Hence proved.

Question 5 :

Find the value of 

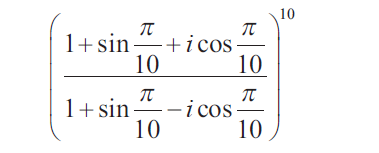
Solution :

Let z  =  sin π/10 + i cos π/10

z bar  =  1/z  =  sin π/10 - i cos π/10

  =  [(1 + z) /  (1 + (1/z))]¹⁰

  =  z¹⁰

  =  [sin π/10 + i cos π/10]¹⁰

  =  [cos [(π/2) - (π/10)] + i sin [(π/2) - (π/10)]]¹⁰

  =  [cos (4π/10) + i sin (4π/10)]¹⁰

  =  [cos 4π + i sin 4π]

  =  1 + i(0)

  =  1

Hence the answer is 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.