QUESTIONS ON SURFACE AREA OF CYLINDER

Question 1 :

A solid right circular cylinder has radius of 14 cm and height of 8 cm. Find its curved surface area and total surface area.

Solution :

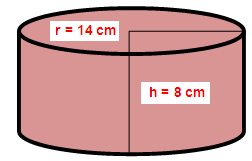
Radius of the cylinder (r) = 14 cm

Height of the cylinder (h) = 8 cm

Curved surface area of cylinder = 2 Π r h

=  2 ⋅ (22/7) ⋅ 14 ⋅ 8

=  2 ⋅ 22 ⋅ 2 ⋅ 8

=  704 sq.cm

Total surface area of cylinder  =  2 Π r (h + r)

=  2 ⋅ (22/7) ⋅ 14 ⋅ (8 + 14)

=  2 ⋅ (22/7)  ⋅ 14 ⋅ 22

=  2 ⋅ 22 ⋅ 2 ⋅ 22

=  1936 sq.cm

Curved surface area = 704 sq.cm

Total surface area = 1936 sq.cm

Question 2 :

The total surface area of a solid circular is 660 sq.m If its diameter of the base is 14 cm. Find the height and curved surface area of the cylinder.

Solution :

Radius of the cylinder  =  14/2  =  7 cm

Total surface area of cylinder  =  660 sq.m

2 Π r (h + r)  =  660 sq.m

2 ⋅ (22/7) ⋅ 7 ⋅ (h + 7)  =  660

h + 7  =  660 ⋅ (1/2) ⋅ (7/22) ⋅ (1/7)

h + 7  =  15

h  =  8 cm

Curved surface area of cylinder = 2 Π r h

=  2 ⋅ (22/7) ⋅ 7⋅ 8

=  352 Sq.cm

Height = 8 cm

Curved surface area = 352 sq.cm

Question 3 :

Curved surface area and circumference at the base of a solid right circular cylinder are 4400 sq.cm and 110 cm respectively. Find its height and diameter.

Solution:

Curved surface area of cylinder  =  4400 sq.cm

Circumference of the base  =  110 cm

2 Π r  =   110

2 ⋅ (22/7) ⋅ r   =  110

r  =  110 ⋅ (1/2) ⋅ (7/22)   

r  =  17.5 cm

diameter  =  2 r

=  2 (17.5)

=  35 cm

2 Π r h  =  4400

110 ⋅ h  =  4400

h  =  4400/110

h  =  40 cm

Height  =  40 cm

Diameter of the cylinder  =  35 cm

Problem 4 :

A tent is of the shape of a right circular cylinder upto a height of 3 meters and then becomes a right circular cone with a maximum height of 13.5 m above the ground. Calculate cost of painting the inner side of the tent at the rate of $2 per square meter, if radius of base is 14 m.

Solution :

Height of cylindrical tent = 3 m

Height of tent = 13.5

height of cylinder + height of cone = 13.5

3 + height of cone = 13.5

height of cone = 13.5 - 3

= 10.5 cm

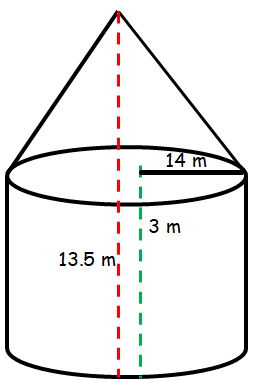
Radius of cylinder = radius of cone = 14 m

Surface area of tent = Surface area of cylinder + surface area of cone

= 2Πrh + Πrl 

= Πr(2h + l) -----(1)

l = √r² + h²

l = √14² + 10.5²

= √196 + 110.25

= √306.25

Slant height (l) = 17.5

Applying all these values in (1), we get

= Π x 14(2(3) + 17.5)

= 3.14 x 14(6 + 17.5)

= 43.96(23.5)

= 1033.06 m²

Cost = $2 per square m

Required cost = 1033.06 x 2

= $2066

Problem 5 :

A solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find volume and total surface area of the solid.

Solution :

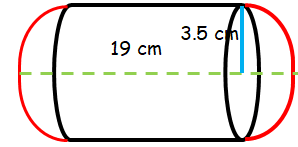
Total height of solid = 19 cm

2 radius of hemisphere + height of cylinder = 19

2(3.5) + height of cylinder = 19

7 + height of cylinder = 19

height of cylinder = 12 cm

Volume of solid :

= Volume of cylinder + 2 volume of hemisphere

= Πr² h + 2(2/3) Πr³

=  Πr² (h + 4/3 r)

=  Π(3.5)² (12 + (4/3) x 3.5)

= 3.14 x 12.25 x (12 + 4.6)

= 38.465(16.6)

= 638.51 cm³

Surface area of solid :

To find total surface area of solid, we add surface area of cylinder by 2 surface area of hemisphere

= 2Πrh + 2 x 2Πr²

= 2Πr(h + 2r)

= 2 x 3.14 x 3.5(12 + 2(3.5))

= 21.98 (12 + 7)

= 21.98(19)

= 417.6

approximately 418 cm²

Problem 5 :

A circus tent is cylindrical upto a height of 3 m and conical above it. If the diameter of the base is 105 m and the slant height of the conical part is 53 m, find the total canvas used in making the tent

Solution :

Height of cylinder = 3 m

Radius of base = 105/2 ==> 52.5

Slant height of conical part = 53

To find the canvas needed to make the tent, we have to find the curved surface area of cylinder and cone.

= 2Πrh + Πrl

= Πr(2h + l)

= 3.14 x 52.5(2(3) + 53)

= 164.85 (6 + 53)

= 164.85(59)

= 9726.15 m²

So, the quantity of canvas required is 9726.15 m²

Problem 6 :

A solid is composed of a cylinder with hemispherical ends. It the whole length of the solid is 104 cm and the radius of each of the hemispherical ends is 7 cm, find area to be polished.

Solution :

Length of solid = 104 cm

The entire length includes radius of two hemispheres and height of cylinder.

2r + height of cylinder = 104

2(7) + height of cylinder = 104

height of cylinder = 104 - 14

= 90

Area to be polished = 2Πrh + 2(2Πr²)

= 2Πr(h + 2r)

= 2 x 3.14 x 7 (90+2(7))

= 43.96 x (90 + 14)

= 43.96 x 104

= 4571.84 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.