RANK OF MATRIX BY MINOR METHOD

Rank of Matrix by Minor Method :

Here we are going to see some example problems to know the method of finding rank of a matrix by minor method.

Rank of Matrix by Minor Method - Examples

The rank of a matrix A is defined as the order of a highest order non-vanishing minor of the matrix A. It is denoted by the symbol ρ (A).The rank of a zero matrix is defined to be 0.

Note

(i) If a matrix contains at-least one non-zero element, then ρ (A) ≥ 1

(ii) The rank of the identity matrix I_n is n.

(iii) If the rank of a matrix A is r, then there exists at-least one minor of A of order r which does not vanish and every minor of A of order r + 1 and higher order (if any) vanishes.

(iv) If A is an m × n matrix, then ρ (A) ≤ min {m, n} = minimum of m, n.

(v) A square matrix A of order n has inverse if and only if ρ (A) = n.

Question 1 :

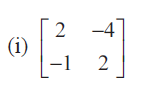
Solution :

Then A is a matrix of order 2×2. So ρ (A)  min {2, 2} = 2. The highest order of minors of A is 2 . There is only one third order minor of A .

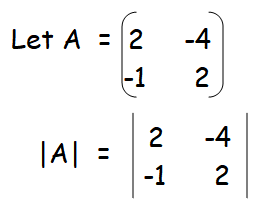
  =  4 - 4 

|A|  =  0

The rank of the given matrix will be less than 2.

Hence the rank of the given matrix is 1.

Question 2 :

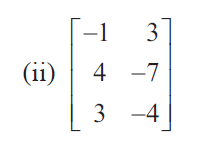
Solution :

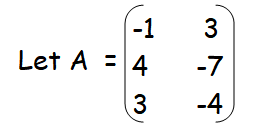
Then A is a matrix of order 3 × 2. So ρ (A)  min {3, 2} = 2. The highest order of minors of A is 2 . 

There are four 2 x 2 minor matrices in the above matrix. By finding the determinants, we get

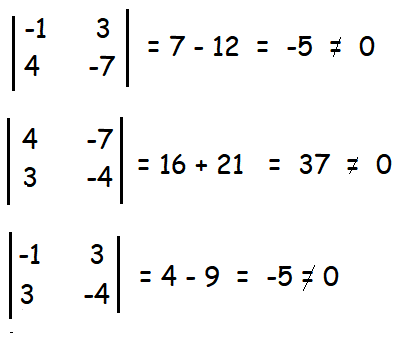
Since the minor of 2 x 2 matrix is not equal to zero, the rank of the given matrix is 2.

Question 3 :

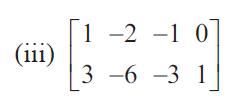
Solution :

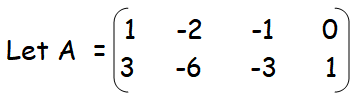
Then A is a matrix of order 2 × 4. So ρ (A)  min {2, 4} = 2. The highest order of minors of A is 2 . 

There are four 2 x 2 minor matrices in the above matrix.

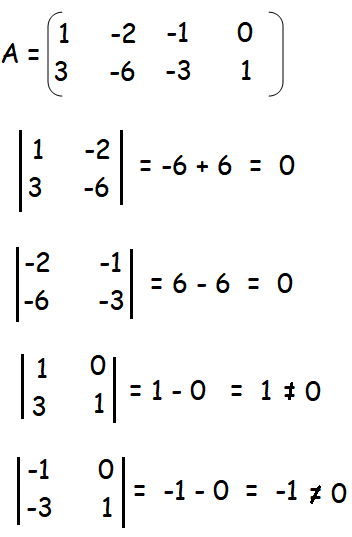
Rank of the given matrix is 2.

Question 4 :

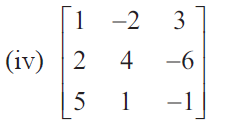
Solution :

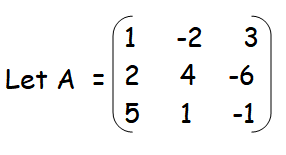
Then A is a matrix of order 3 × 3. So ρ (A)  min {3, 3} = 3. The highest order of minors of A is 3 . 

By finding determinant of given matrix, we get 

  =  1(-4 + 6) + 2(-2 + 30) + 3(2 - 20)

  =  1(2) + 2(28) + 3(-18)

  =  2 + 56 - 54

  =   58 - 54

|A|  =  4 ≠ 0

Hence the rank of the given matrix is 3.

Question 5 :

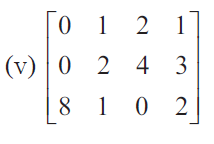
Solution :

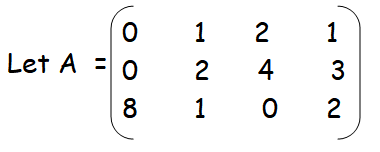
Then A is a matrix of order 3 × 4. So ρ (A)  min {3, 4} = 3. The highest order of minors of A is 3 . 

By finding determinant of given matrix, we get 

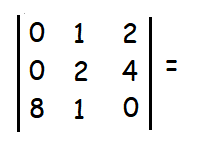	0(0 - 4) - 1(0-32) + 2(0-16)   =  0 - 1(-32) + 2(-16)   =  32 - 32   =  0
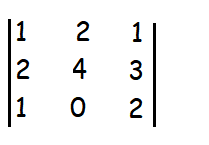	=  1(8-0) - 2(4-3) + 1(0-4)   =  8 - 2(1) + 1(-4)   =  8 - 2 - 4   =  8 - 6   =  2 ≠ 0

Hence the rank of the given matrix is 3.

After having gone through the stuff given above, we hope that the students would have understood, "Rank of Matrix by Minor Method". 

Apart from the stuff given in this section "Rank of Matrix by Minor Method", if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.