RATE TIME DISTANCE PROBLEMS

In this section, we will learn how to solve word problems that involve the distance an object will travel at a certain average rate for a given period of time.

We can use the formulas given below to solve problems on distance, time and rate.

Distance, Time and Rate - Formulas

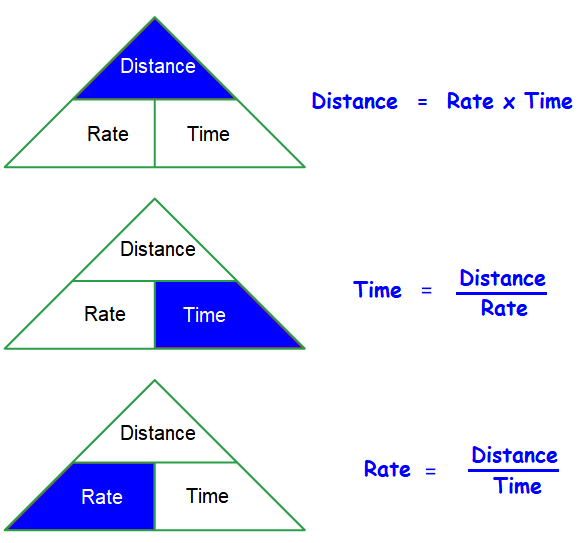
Solved Problems

Problem 1 :

If a person travels at a rate of 40 miles per hour. At the same rate, how long will he take to cover 160 miles distance?

Solution :

Given : Rate is 40 miles per hour.

The formula to find the time when distance and rate are given is

Time  =  Distance / Rate

Time taken to cover the distance of 160 miles is 

Time  =  160 / 40

Time  =  4 hours

So, the person will take 4 hours to cover 160 miles distance at the rate of 40 miles per hour.    

Problem 2 :

A person travels at a rate of 60 km per hour. Then how many meters can he travel in 5 minutes ?

Solution :

Given : Rate is 60 km per hour.

The distance covered in 1 hour or 60 minutes is 

=  60 km

=  60 ⋅ 1000 meters

=  60000 meters

Then the distance covered in 1 minute is

=  60000 / 60

=  1000 m

The distance covered in 5 minutes is

=  5 ⋅ 1000 

=  5000 meters

So, the person can cover 5000 meters distance in 5 minutes.   

Problem 3 :

Bicyclists Bryan and Jack started at noon from points 60 km apart and rode toward each other, meeting at 1:30 p.m. Bryan's speed was 4 km/h greater than Jack's speed. Find their speeds. 

Solution :

Step 1 :

Begin with drawing a sketch. 

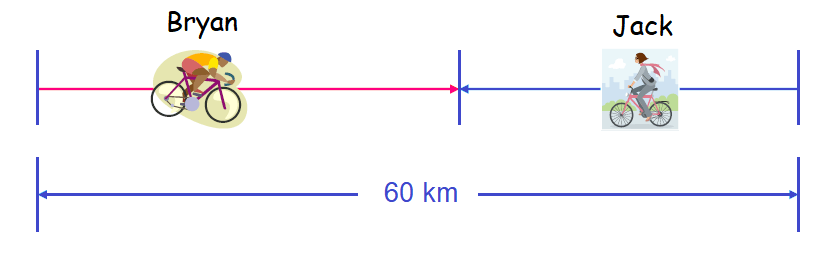
Step 2 :

Let r = Jack's speed. 

Then, Bryan's speed  =  (r + 4).

Both started at noon (12:00 p.m) and meeting each other at 1 : 30 p.m.

So, both of them take 1.5 hours time to meet each other from their starting points.  

Prepare a chart organizing the given facts and use it to label the sketch. 

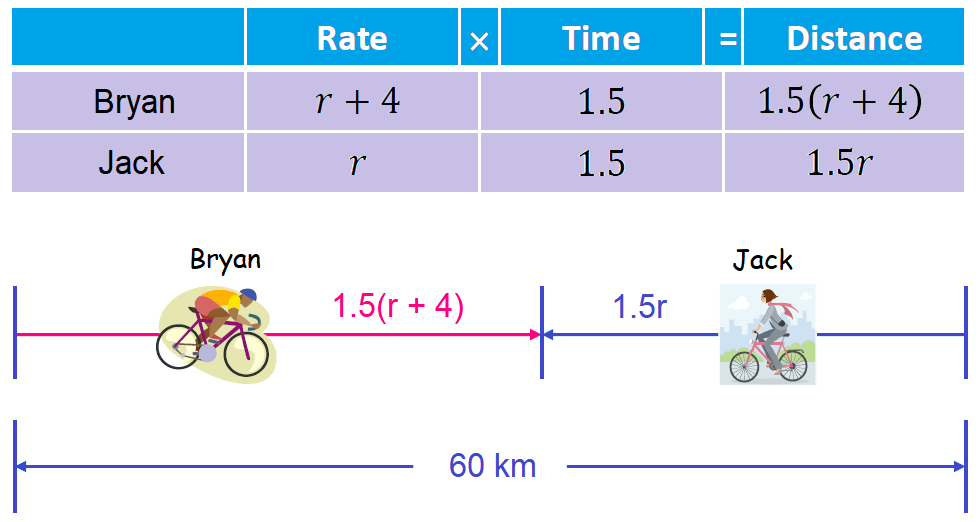
Step 3 : 

Based on the sketch and information in step 2, we can form equation as shown below. 

1.5(r + 4) + 1.5r  =  60

Step 4 :

Solve the equation in step 3 for r.

1.5(r + 4) + 1.5r  =  60

Simplify. 

1.5r + 6 + 1.5r  =  60

3r + 6  =  60

Subtract 6 from each side. 

3r  =  54

Divide each side by 3.

r  =  18

r + 4  =  18 + 4  =  22

So, Jack's speed is 18 km/hr and Bryan speed is 22 km/hr. 

Problem 4 :

A helicopter leaves Airport and flies north at 180 mi/h. Twenty minutes later a plane leaves the same airport and follows the helicopter at 330 mi/h. How long does it take the plane to overtake the helicopter ?

Solution :

Step 1 :

Begin with drawing a sketch. 

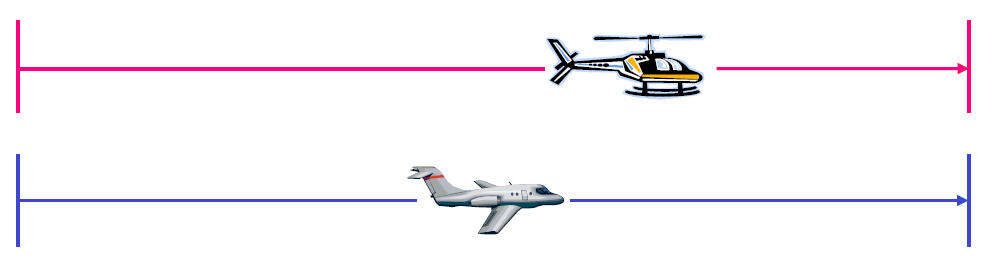
Step 2 :

Let t  =  plane's flying time. 

Because the speeds are given in miles per hour, we have to write 20 minutes as 1/3 hours. 

Then, helicopter's flying time  =  (t + 1/3).

Prepare a chart organizing the given facts and use it to label the sketch. 

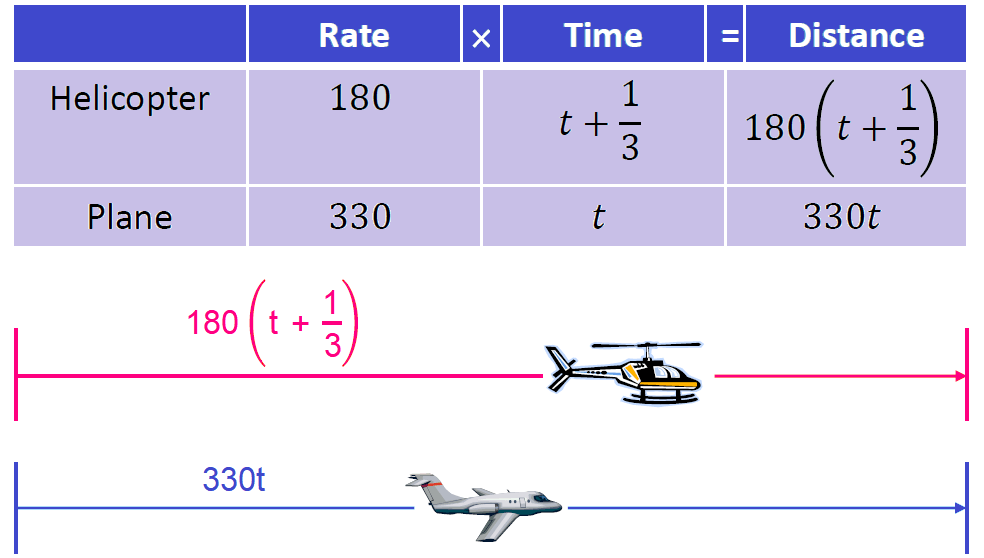
Step 3 :

At the point where the plane overtakes the helicopter, the distance covered by the plane and helicopter will be equal.

Using distance formula, we have

330t  =  80(t + 1/3)

Step 4 :

Solve the equation in step 3 for t.

330t  =  180(t + 1/3)

Simplify. 

330t  =  180t + 60 

Subtract 180t from each side. 

150t  =  60

Divide each side by 150.

t  =  60 / 150

t  =  2/5 hours

t  =  2/5 ⋅ 60 minutes

t  =  24 minutes   

So, the plane overtakes the helicopter in 24 minutes. 

Problem 5 :

A ski lift carried  up a slope at the rate of 6 km/h. and she skied back down parallel to the lift at 34 km/h. The round trip took 30 min. How far did she ski and for how long ?

Solution :

Step 1 :

Begin with drawing a sketch. 

Step 2 :

Let t = Lily's skiing time. 

Because the speeds are given in miles per hour, we have to write 30 minutes as 1/2 or 0.5 hours. 

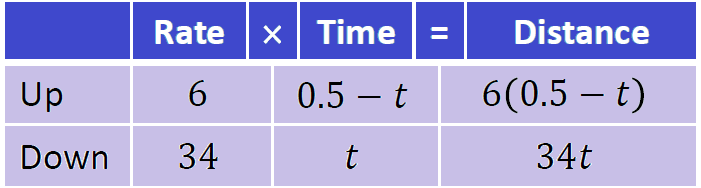
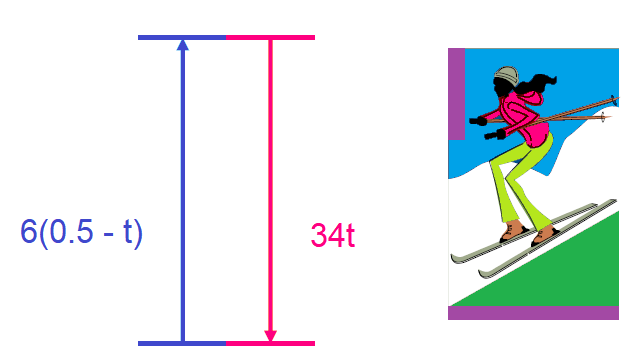
Step 3 :

In a round-trip, the two distances covered are equal.

Using distance formula, we have

34t  =  6(0.5 - t)

Step 4 :

Solve the equation in step 3 for t.

34t  =  6(0.5 - t)

Simplify. 

34t  =  3 - 6t

Add 6t to each side. 

40t  =  3

Divide both sides by 40. 

t  =  3/40

t  =  0.075 hours

t  =  0.075 ⋅ 60 minutes

t  =   4.5 minutes

Distance covered :

=  Rate ⋅ Time

Substitute, Rate  =  34 and Time  =  0.075 

=  34 ⋅ 0.075

=  2.55 km

So, Maria skied for 0.075 h. or 4.5 min. for a distance of 2.55 km.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.