RATIONAL NUMBERS BETWEEN 3 AND 4

In this section, we will learn how to find rational numbers (a/b, b ≠ 0) between 3 and 4 using the formula method.

Formula Method

Let ‘a’ and ‘b’ be any two given rational numbers. We can find many rational numbers q1, q2, q3,...in between a and b as follows :

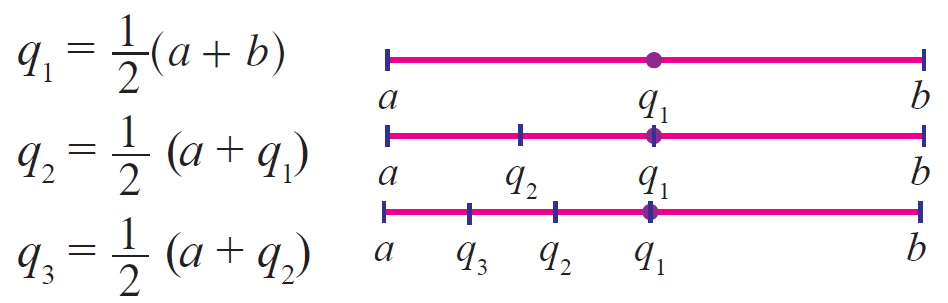
The numbers q2, q3 lie to the left of q1. Similarly, q4, q5 are the rational numbers between ‘a’ and ‘b’ lie to the right of q1 as follows:

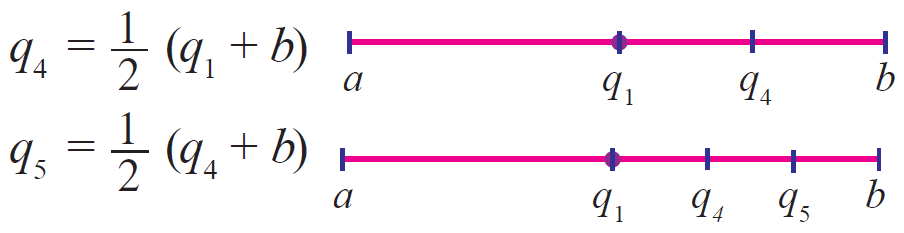
Important Note : 

Average of two numbers always lies between them.

Rational Numbers between 3 and 4

Now, let us find rational numbers between 3 & 4

Solution : 

Let a = 3 and b = 4

Let q1, q2, q3, q4, q5,.......... be the rational number between 3 and 4. 

Then, we have 

q1  =  1/2 x (a + b)

q1  =  1/2 x (3 + 4)

q1  =  1/2 x (7)

q1  =  7/2

Let q2 be the rational number between 3 and 7/2

Then, we have 

q2  =  1/2 x (3 + 7/2)

q2  =  1/2 x 13/2

q2  =  13/4

Let q3 be the rational number between 3 and 13/4

Then, we have 

q3  =  1/2 x (3 + 13/4)

q3  =  1/2 x 25/4

q3  =  25/8

Let q4 be the rational number between 3 and 25/8

Then, we have 

q4  =  1/2 x (3 + 25/8)

q4  =  1/2 x 49/8

q4  =  49/16

Let q5 be the rational number between 3 and 49/16

Then, we have 

q5  =  1/2 x (3 + 49/16)

q5  =  1/2 x 97/16

q5  =  97/32

Let q6 be the rational number between 3 and 97/32

Then, we have 

q6  =  1/2 x (3 + 97/32)

q6  =  1/2 x 193/32

q6  =  193/64

In this way, we can find many rational numbers between 3 & 4 as given below.

3 < 193/64 < 97/32 < 49/16 < 25/8 < 13/4 < 7/2 < 4

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.