RATIONAL NUMBERS BETWEEN TWO RATIONAL NUMBERS

Let us consider the two rational numbers a/b and c/d. Here a, b, c and d are integers and also b ≠ 0, d ≠ 0. 

We can find many rational numbers between a/b and c/d using the two methods given below.

1. Formula method

2. Same denominator method

Formula Method

Let ‘a’ and ‘b’ be any two given rational numbers. We can find many rational numbers q1, q2, q3,...in between a and b as follows :

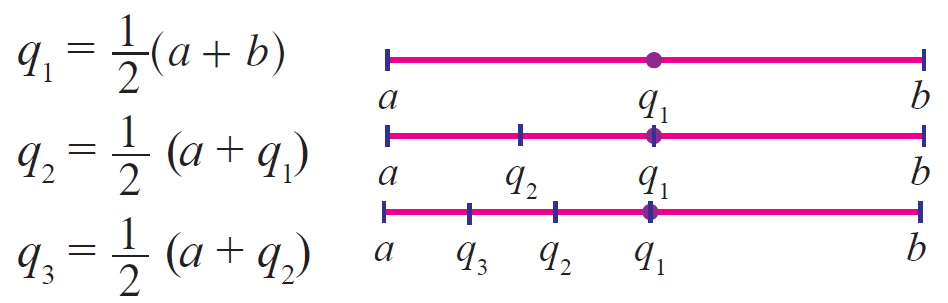
The numbers q2, q3 lie to the left of q1. Similarly, q4, q5 are the rational numbers between ‘a’ and ‘b’ lie to the right of q1 as follows:

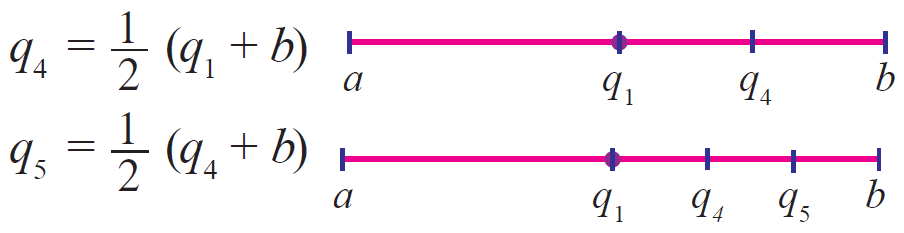
Important Note : 

Average of two numbers always lies between them.

Same Denominator Method

Let ‘a’ and ‘b’ be two rational numbers.

(i) Convert the denominator of both the fractions into the same denominator by taking LCM. Now, if there is a number between numerators there is a rational number between them.

(ii) If there is no number between their numerators, then multiply their numerators and denominators by 10 to get rational numbers between them.

To get more rational numbers, multiply by 100, 1000 and so on.

Important Note : 

By following different methods one can get different rational numbers between ‘a’ and ‘b’.

Rational Numbers between Two Rational Numbers

Example 1 :

Find a rational number between 3/4 and 4/5

Solution : 

Formula Method : 

Let a = 3/4 and b = 4/5

Let q be the rational number between 3/4 and 4/5. 

Then, we have 

q  =  1/2 x (a + b)

q  =  1/2 x (3/4 + 4/5)

q  =  1/2 x (15 + 16) / 20

q  =  1/2 x 31/20

q  =  31/40

So, the rational number between 3/4 and 4/5 is 31/40.

Same Denominator Method :

Let a = 3/4 and b = 4/5

L.C.M of the denominator (4, 5) is 20.

So, we can write "a" and "b" as given below

a  =  3/4 x 5/5  =  15/20

and

b  =  4/5 x 4/4  =  16/20 

To find a rational number between 15/20 and 16/20 , we have to multiply the numerator and denominator by 10.

Then, we have

15/20 x 10/10  =  150/200

16/20 x 10/10  =  160/200

Therefore, the rational numbers between 150/200 and 160/200 are 151/200, 152/200, 153/200, 154/200, 155/200, 156/200, 157/200, 158/200 and 159/200.

Example 2 :

Find two rational numbers between -3/5 and 1/2.

Solution : 

Let a = -3/5 and b = 1/2

Let q1 and q2 be the rational number between -3/5 and 1/2. 

First, let us get q1.

q1  =  1/2 x (a + b)

q1  =  1/2 x (-3/5 + 1/2)

q1  =  1/2 x (-6 + 5) / 10

q1  =  1/2 x (-1/10)

q1  =  -1/20

Now, let find q2.

q2  =  1/2 x (a + q1)

q2  =  1/2 x (-3/5 - 1/20)

q2  =  1/2 x (-12 - 1) / 20

q2  =  1/2 x (-13/20)

q2  =  -13/40

So, the two rational number are -1/20 and -13/40.

Note : 

The two rational numbers can be inserted as 

-3/5 < -13/40 < -1/20 < 1/2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.