REAL NUMBER SYSTEM

In the development of science, we should know about the properties and operations on numbers which are very important in our daily life.

In the earlier classes we have studied about the whole numbers and the fundamental operations on them.

Now, we extend our study to the integers, rational numbers, decimals, fractions and powers in this section. 

The picture given below clearly illustrates the real number system.

Numbers

In real life, we use Hindu Arabic numerals - a system which consists of the symbols 0 to 9.

This system of reading and writing numerals is called, 'Base ten system' or 'Decimal number system'.

Natural Numbers

Counting numbers are called natural numbers. These numbers start with smallest number 1 and go on without end. The set of all natural numbers is denoted by the symbol N.

N = {1, 2, 3, 4, 5, .......} is the set of all natural numbers.

Whole Numbers

Natural numbers together with zero (0) are called whole numbers. These numbers start with smallest number 0 and go on without end.

The set of all whole numbers is denoted by the symbol W.

W = {0, 1, 2, 3, 4, 5, .......} is the set of all whole numbers.

Integers

The whole numbers and negative numbers together are called integers.

The set of all integers is denoted by Z.

Z = {...- 2, - 1,0,1,2,...,} is the set of all integers.

Fractions

A fraction is a part or parts of a whole.

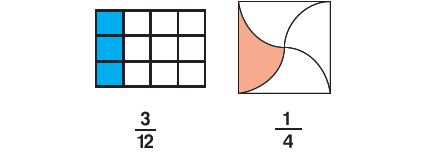
In a fraction, the number above the line is called the numerator and the number below the line is called the denominator.

Fraction = Numerator/Denominator

Decimal Numbers

A number in which we have 'point' is called as decimal number. 

A decimal number has two parts namely an integral part and a decimal part. 

Examples :

1)  Let us consider the decimal number 0.6.

0.6 can be written as 0 + 0.6.

Here, integral part  =  0 and decimal part  =  6.

2)  Let us consider the decimal number 7.2.

7.2 can be written as 7 + 0.2.

Here, integral part  =  7 and decimal part  =  2.

In a decimal number the digits to the left of the decimal point is the integral part.

The digits to the right of the decimal point is the decimal part. 

The value of all the decimal parts is less than 1.  

Rational Numbers

A rational number is one of the types of of real numbers that is in the form p/q, where q ≠ 0.

Examples of rational number :

5,  2.3,  0.02, 5/6

Because all these numbers can be written as fractions.  

5 = 5/1 

2.3 = 23/10

0.02 = 2/100 = 1/50

5/6 (This is already a fraction)

Apart from the above examples, sometimes we will have recurring decimals like 1.262626..........

1.262626...... is a non terminating recurring decimal.

All these recurring decimals can be converted into fractions and they are also rational numbers.

Important note : 

All the fractions and decimal numbers will come under this category.

Hence, all the fractions and decimal numbers to be considered as rational numbers.

Irrational Numbers

A number which can not be converted into fraction is called as irrational numbers.

Examples of irrational number :

√2 = 1.4142135623.......

√3 = 1.7320508075.......

√26 = 5.099019513.......

All the above non terminating numbers can not be converted into fractions.

Because, they do not have repeated patterns.

When we are trying to find square of a number which is not a perfect square, we get this non repeating non terminating decimal.

And these non recurring decimals can never be converted to fractions and they are called as irrational numbers. 

Note :

A recurring decimal can be converted to a fraction and it is rational.

Click here to know how to convert recurring decimals to fractions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.