REAL WORLD PROBLEMS ON PYTHAGOREAN THEOREM

Problem 1 :

A man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point?

Solution :

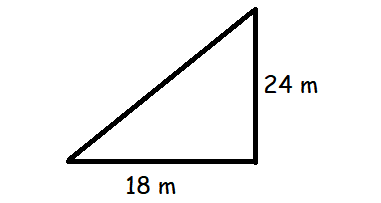
the distance of his current position from the starting point  =  √18² + 24²

  =  √(324 + 576)

  =  √900

  =  30 m

So, the required distance is 30 m.

Problem 2 :

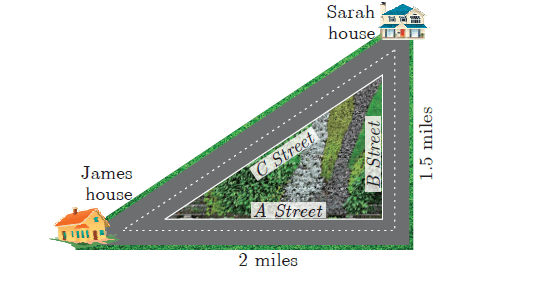
There are two paths that one can choose to go from Sarah’s house to James house. One way is to take C street, and the other way requires to take A street and then B street. How much shorter is the direct path along C street? (Using figure).

Solution :

By choosing the C street, he has to cover the distance,

 =  √2² + 1.5²

 =  √(4 + 2.25)

 =  √6.25

 =  2.5 miles

By choosing the alternative way, he has to cover the distance  =  2 + 1.5

=  3.5 miles

The difference between these two paths =  3.5 - 2.5

  =  1 mile

So, by choosing the direct path, he may save 1 miles faster than other way.

Problem 3 :

To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41 m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?

Solution :

By drawing the rough picture using the given information, we get 

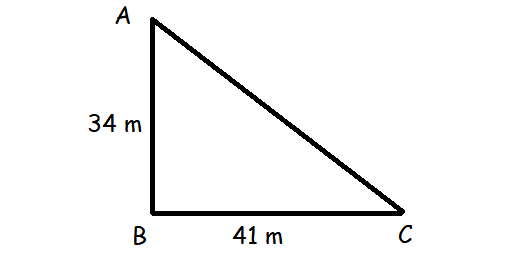
AC  =  √34² + 41²

   =  √1156 + 1681

  =  √2837

  =  53.26

Miles saved  =  (34 + 41) - 53.26

  =  75 - 53.26

=  21.74 m

Problem 4 :

In the rectangle WXYZ, XY + YZ = 17 cm, and XZ + YW = 26 cm. Calculate the length and breadth of the rectangle?

Solution :

XY + YZ = 17 cm

XZ + YW = 26 cm

To calculate : - Length and breadth of the rectangle.

We know that,

Diagonals of a rectangle are equal.

So,

XZ = YW

Then,

XZ = YW = 26/2 = 13 cm

In ∆XYZ, let YZ = P. Then

XY = 17 - P

Then, by Pythagoras theorem,

(P)² + (17 - P)² = (13)²

P² + 289 - 34P + P² = 169

2P² - 34P = 169 - 289

2(P² - 17P) = - 120

 P² - 17P = - 120/2

P² - 17P = - 60

P² - 17P + 60 = 0

P² - 12P - 5P + 60 = 0

 P(P - 12) - 5(P - 12) = 0

(P - 12)(P - 5) = 0

P - 12  =  0  or  P  =  12

P  =  12 cm  or  P  =  5 cm

Now,

YZ = P = 12 cm [Because , YZ is the length of the rectangle ,so we will assign it the greatest value of P]

Again, XY = (17 - P) = (17 - 12) cm = 5 cm

[Because , XY is thee breadth]

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.