REASONING AND PROOF WORKSHEET

Problem 1 :

Sketch the next figure in the pattern.

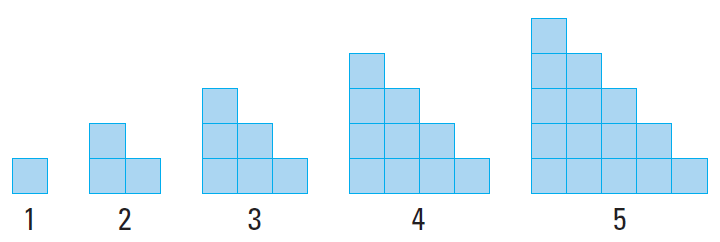
Problem 2 :

Write (a) inverse, (b) converse, (c) contrapositive of the following statement. 

Statement :

"If there is snow on the ground, then the flowers are not in bloom"   

Problem 3 :

Each of the following statements is true. Write the converse of each statement and decide whether the converse is true or false. If the converse is true, combine it with the original statement to form a true biconditional statement. If the converse is false, state a counterexample.

(i) If two points lie in a plane, then the line containing them lies in the plane.

(ii) If a number ends in 0, then the number is divisible by 5.

Problem 4 :

Let p be "the value of x is -5" and let q be "the absolute value of x is 5".

(i) Write p -> q in words.

(ii) Write q -> p in words.

(iii) Decide whether the biconditional statement p <-> q is true.

Problem 5 :

Solve 52y - 3(12 + 9y)  =  64 and write a reason for each step.

Problem 6 :

In the diagram given below, Q is the midpoint of PR.

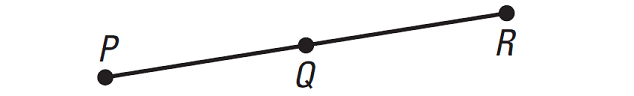
Show that PQ and QR are each equal to 1/2 ⋅ PR.

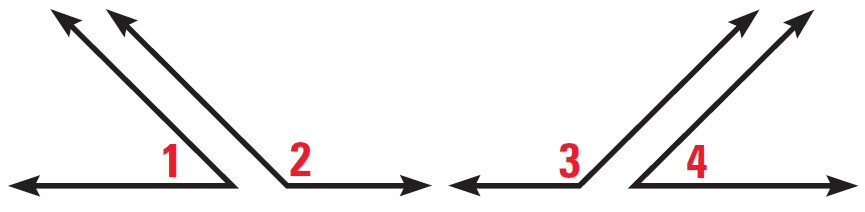
Problem 7 :

In the diagram shown below,

∠1 and ∠2 are supplements,

∠3 and ∠4 are supplements,

∠1 ≅ ∠4

Prove ∠2 ≅ ∠3

1. Answer :

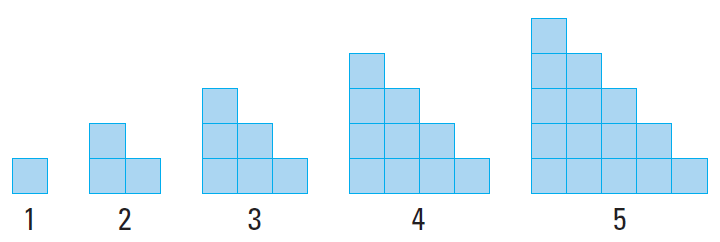
Each figure in the pattern looks like the previous figure with another row of squares added to the bottom. Each figure looks like a stairway. 

So, the sixth figure in the pattern must have six squares in the bottom row.  

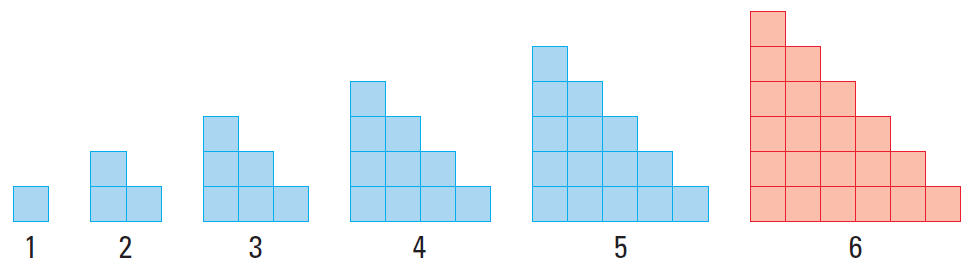
2. Answer :

(a) Inverse : 

"If there is no snow on the ground, then the flowers are in bloom" 

(b) Converse : 

"If flowers are not in bloom, then there is snow on the ground"

(b) Contrapositive : 

"If flowers are in bloom, then there is no snow on the ground"

3. Answer :

Solution (i) :

Converse :

(i) If a line containing two points lies in a plane, then the points lie in the plane.

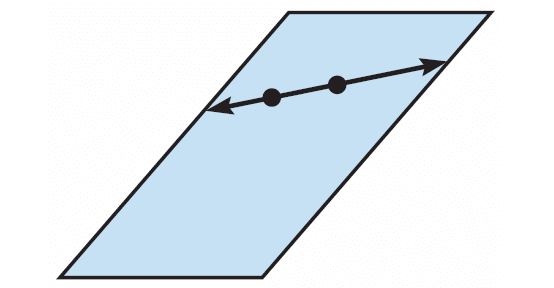
The converse is true, as shown in the diagram. So, it can be combined with the original statement to form the true biconditional statement written below.

Biconditional statement :

Two points lie in a plane, if and only if the line containing them lies in the plane.

Solution (ii) :

Converse :

If a number is divisible by 5, then the number ends in 0. The  converse is false. As a counterexample, consider the number 15. It is divisible by 5, but it does not end in 0, as shown below.

20 ÷ 5  =  4

25 ÷ 5  =  5

30 ÷ 5  =  6

4. Answer :

(i) If the value of x is -5, then the absolute value of x is 5.

(ii) If the absolute value of x is 5, then the value of x is -5.

(iii) The conditional statement in part (a) is true, but its converse in part (b) is false. So, the biconditional statement p <-> q is false. 

5. Answer :

Given :

52y - 3(12 + 9y)  =  64

Distributive Property :

Distribute 3 to 12 and 9y. 

52y - 36 - 27y  =  64

Simplify :

25y - 36  =  64

Addition property of equality : 

Add 36 to each side. 

25y  =  100

Division property of equality : 

Divide both sides by 25. 

y  =  4

6. Answer :

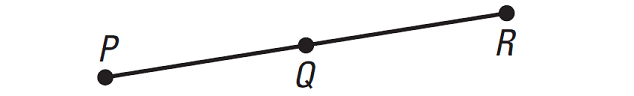
Given : Q is the midpoint of PR

Prove : PQ  =  1/2 ⋅ PR and QR  =  1/2 ⋅ PR

7. Answer :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.