RECIPROCAL RELATION OF TRIGONOMETRIC RATIOS
In the six trigonometric ratios sin, cos, tan, csc, sec and cot, there is a reciprocal relation among them.
Here, the pairs of trigonometric relations are given between which we have reciprocal relation.
sinθ <----> cscθ
cosθ <----> secθ
tanθ <----> cotθ
That is,
|
sinθ = 1/cscθ cosθ = 1/secθ tanθ = 1/cotθ tanθ = sinθ/cosθ |
cscθ = 1/sinθ secθ = 1/cosθ cotθ = 1/tanθ cotθ = cosθ/sinθ |
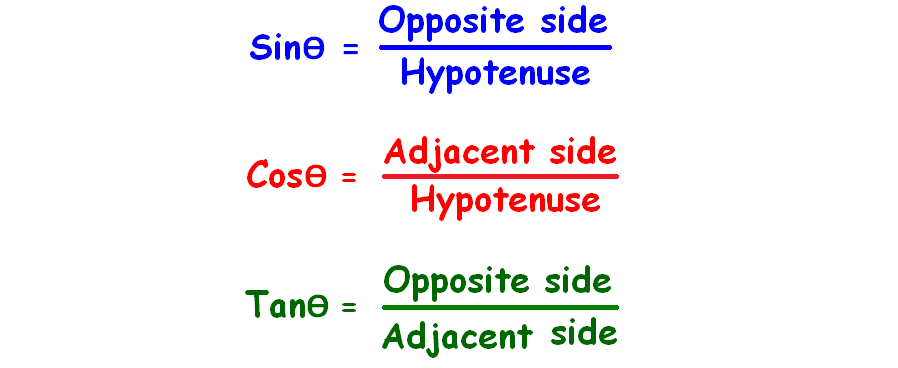
To have better understanding on reciprocal relations of trigonometric ratios, first we have to know the shortcut SOHCAHTOA which is related to the trigonometric ratios sin, cos and tan.
To understand the shortcut, first we have to divide SOHCAHTOA in to three parts as given below.
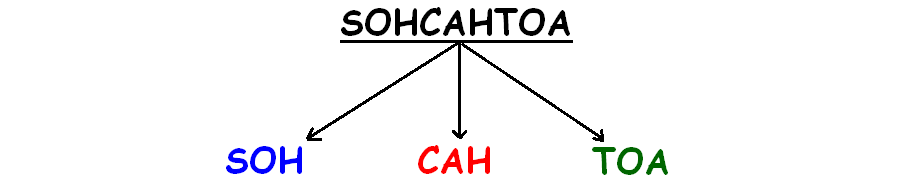
What do SOH, CAH and TOA stand for ?
Here is the answer.
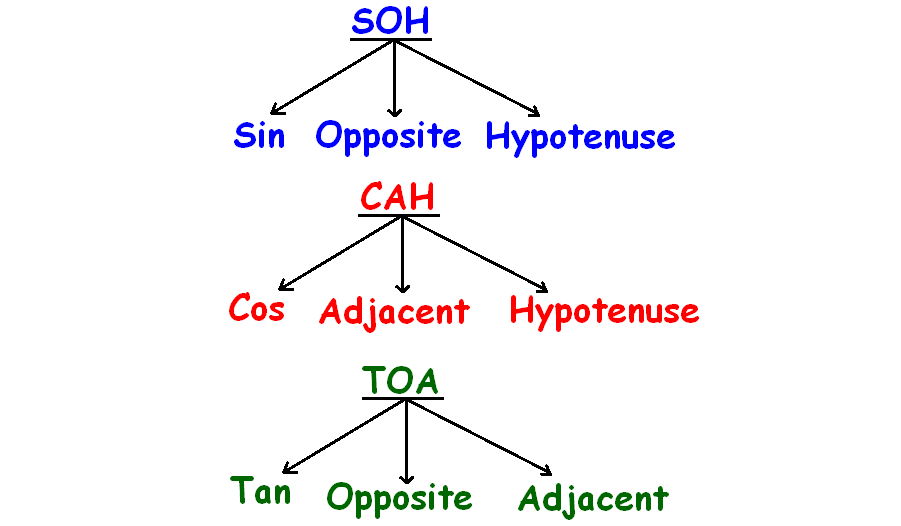
From the above figures, we can derive formulas for the three trigonometric ratios sin, cos and tan as given below.
Solved Problems
Problem 1 :
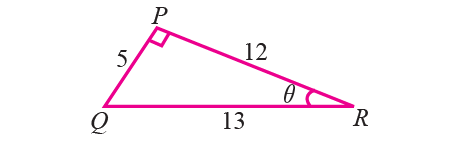
In the right triangle PQR shown below, find the values of sinθ, cosθ and tanθ. Using those values, find the values of cscθ, secθ and cotθ.
Solution :
From the triangle shown above,
opposite side = 5
adjacent side = 12
hypotenuse = 13
Therefore,
|
sinθ = PQ/RQ = 5/13 cosθ = PR/RQ = 12/13 tanθ = PQ/PR = 5/12 |
cscθ = 1/sinθ = 13/5 secθ = 1/cosθ = 13/12 cotθ = 1/tanθ = 12/5 |
Problem 2 :
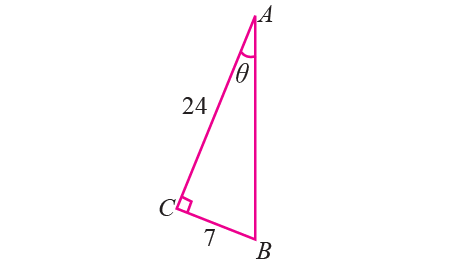
In the right triangle ABC shown below, find the values of sinθ, cosθ and tanθ. Using those values, find the values of cscθ, secθ and cotθ.
Solution :
From the right triangle shown above,
AC = 24
BC = 7
By Pythagorean Theorem,
AB2 = BC2 + CA2
AB2 = 72 + 242
AB2 = 49 + 576
AB2 = 625
AB2 = 252
AB = 25
Now, we can use the three sides to find the six trigonometric ratios of angle θ.
Therefore,
|
sinθ = BC/AB = 7/25 cosθ = AC/AB = 24/25 tanθ = BC/AC = 7/24 |
cscθ = 1/sinθ = 25/7 secθ = 1/cosθ = 24/25 cotθ = 1/tanθ = 24/7 |
Problem 3 :
In triangle ABC, right angled at B, 15sinA = 12. Find the six trigonometric ratios of angle A and C.
Solution :
Given : 15sinA = 12.
sinA = 12/15
sinA = 4/5
Therefore,
opposite side = 4
hypotenuse = 5
Let us consider the right triangle ABC where right angled at B, with
BC = 12
AC = 15
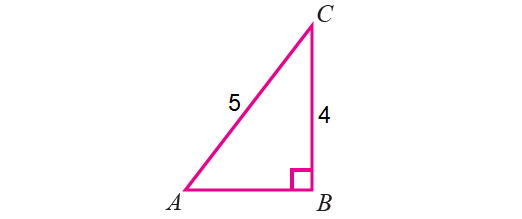
By Pythagorean theorem,
AC2 = AB2 + BC2
52 = AB2 + 42
25 = AB2 + 16
25 - 16 = AB2
9 = AB2
32 = AB2
3 = AB
Now, we can use the three sides to find the five trigonometric ratios of angle A and six trigonometric ratios of angle C.
Therefore,
|
sinA = 4/5 cosA = AB/AC = 3/5 tanA = BC/AB = 4/3 sinC = AB/AC = 3/5 cosC = BC/AC = 4/5 tanC = AB/BC = 3/4 |
cscA = 1/sinA = 5/4 secA = 1/cosA = 5/3 cotA = 1/tanA = 3/4 cscC = 1/sinC = 5/3 secC = 1/cosC = 5/4 cotC = 1/tanC = 4/3 |
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Permutation Problems with Solutions
May 08, 25 12:28 PM
Permutation Problems with Solutions -
Digital SAT Math Problems and Solutions (Part - 159)
May 08, 25 01:39 AM
Digital SAT Math Problems and Solutions (Part - 159) -
Digital SAT Math Problems and Solutions (Part - 158)
May 06, 25 11:00 AM
Digital SAT Math Problems and Solutions (Part - 158)