REFERENCE ANGLE

Let A be an angle in standard position. The reference angle B associated with A is the acute angle formed by the terminal side of A and the x-axis.

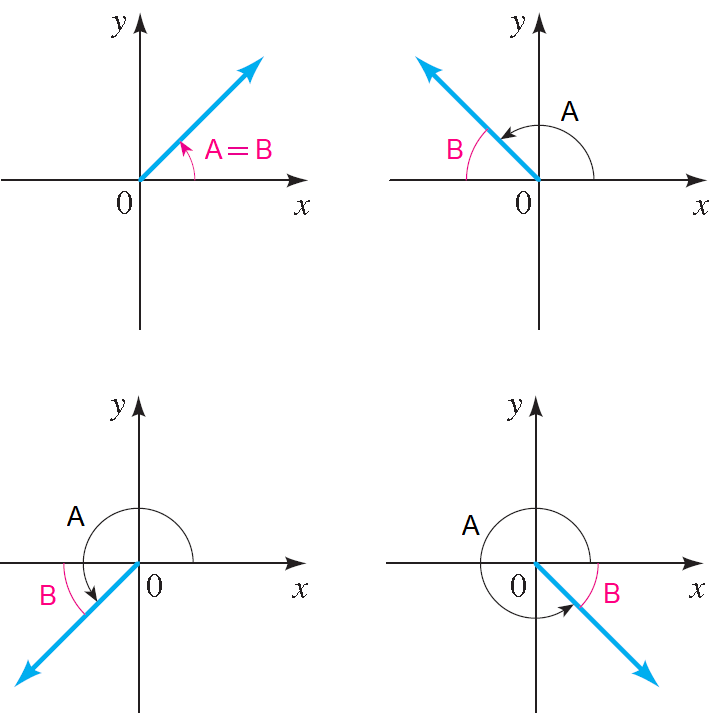
Working Rule to Find Reference Angle

Ensure that the given angle is positive and it is between 0° and 360°.

What if the given angle does not meet the criteria above :

Let θ be the angle given.

Case 1 :

If θ is positive but greater than 360°, find the positive angle between 0° and 360° that is coterminal with θ°.

To get the coterminal angle, divide θ by 360° and take the remainder.

Case 2 :

If θ is negative, add multiples of 360° to θ make the angle as positive such that it is between 0° and 360°.

Once we have the given angle as positive and also it is between 0° and 360°, easily we can find the reference angle as explained below.

Let A be a positive angle such that 0° < A < 360°.

1. When A is in quadrant I,

reference angle = A

2. When A is in quadrant II,

reference angle = π - A or 180° - A

3. When A is in quadrant III,

reference angle = A - π  or A - 180°

4. When A is in quadrant IV,

reference angle = 2π - A or 360° - A

Division of Quadrants

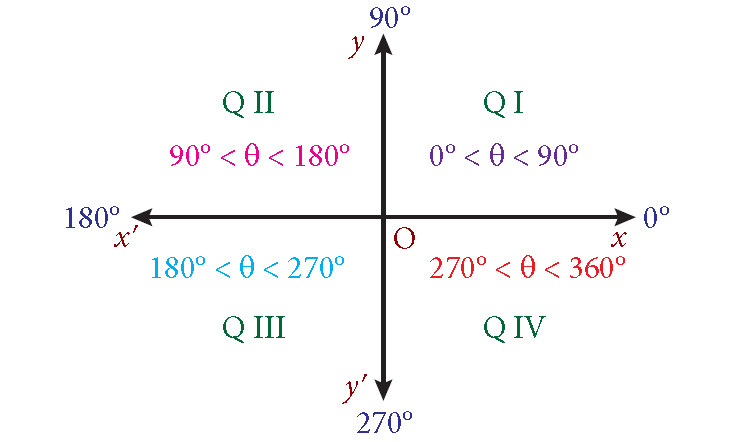
Figures given in the following examples show that to find a reference angle it’s useful to know the quadrant in which the terminal side of the angle lies.

Example 1 :

Find the reference angle for 5π/3.

Solution :

The given angle 5π/3 (or 150°) is less than 2π (or 360°).

The reference angle is the acute angle formed by the terminal side of the angle 5π/3 and the x-axis (see the figure shown below).

The angle 5π/3 has its terminal side in quadrant IV, as shown below.

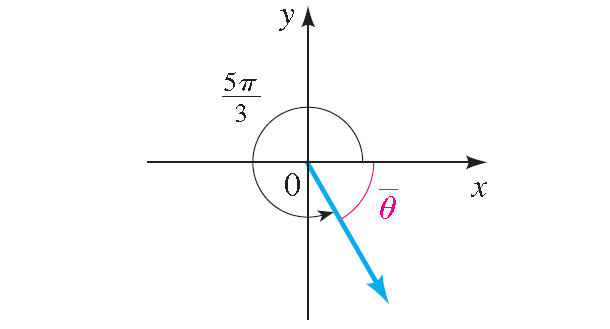
So, the reference angle is

= 2π - 5π/3

= π/3

Example 2 :

Find the reference angle for 240°.

Solution :

The given angle 240° is less than 360°.

The angle 240° has its terminal side in quadrant III, as shown below.

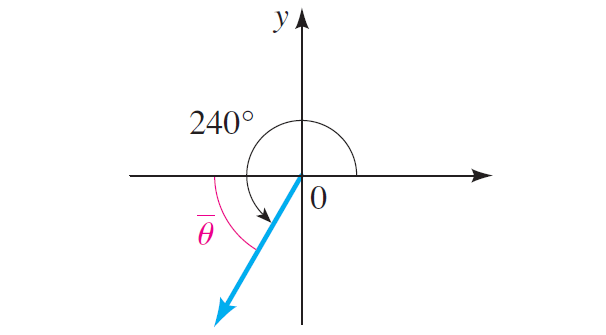
So, the reference angle is

= 240° - 180°

= 60°

Example 3 :

Find the reference angle for 870°.

Solution :

The given angle 870° is greater than 360°.

Find the positive angle between 0° and 360° that is coterminal with 870°.

Divide 870° by 360° and take the remainder.

870° ÷ 360° ---> Remainder = 150°

The positive angle between 0° and 360° that is coterminal with 870° is 150°.

The angle 150° has its terminal side in quadrant III, as shown below.

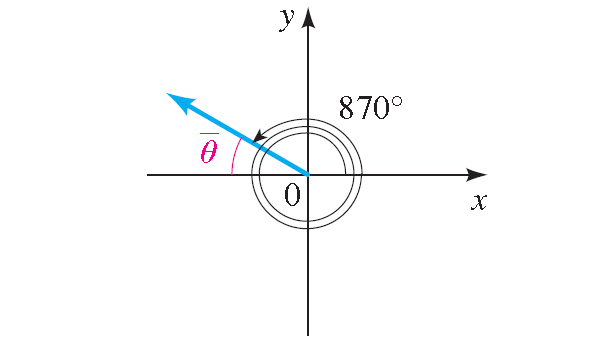
So the reference angle is

= 180° - 150°

= 30°

Example 4 :

Find the reference angle for 8π/3.

Solution :

The given angle 8π/3 is greater than 2π.

Find the positive angle between 0 and 2π that is coterminal with 8π/3.

To make the process easier, convert 8π/3 radians to degrees.

8π/3 = 8(180°)/3 = 480°

Divide 480° by 360° and take the remainder.

480° ÷ 360° ---> Remainder = 120°

The terminal side of the angle 120° is in quadrant II.

120° ⋅ π/180° = 2π/3 radians

So, the reference angle is

= π - 2π/3

= π/3

Example 5 :

Find the reference angle for -135°.

Solution :

The given angle -135° is negative.

Add multiples of 360° to -135° to make the angle as positive such that it is between 0° and 360°.

-135° + 360° = 225°

225° is positive and less than 360°.

The terminal side of the angle 225° is in quadrant III.

So, the reference angle is

= 225° - 180°

= 45°

Example 6 :

Find the reference angle for -13π/4.

Solution :

The given angle -13π/4 is negative.

Add multiples of 2π to -13π/4 to make the angle as positive such that it is between 0 and 2π.

-13π/4 + 2(2π) = -13π/4 + 4π = 3π/4

3π/4 is positive and less than 2π.

The terminal side of the angle 3π/4 (or 135°) is in quadrant II.

So, the reference angle is

= π - 3π/4

= π/4

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.