REFLECTING A GRAPH IN THE HORIZONTAL OR VERTICAL AXIS

The procedure for reflecting the graph of a function through the horizontal axis is illustrated by the following examples:

Question 1 :

Define a function g by 

g(x) = −f(x)

where f is the function defined by f(x) = x², with the domain of f the interval [−1, 1].

(a) Find the domain of g.

(b) Find the range of g.

(c) Sketch the graph of g.

Solution :

From the given question g(x)  =  - f(x), we come to know that, we have to perform horizontal reflection.

(a)  According to the definition domain of both functions will be same. So the domain of g(x) is [-1, 1]

(b)  To find the range of g, let us find the range of f(x) using the domain [-1, 1].

 f(x) = x²

If x = -1, then y = 1

If x = 0, then y = 0

If x =-1, then y = 1

Range of f(x) is [0, 1]. The range of g(x) can be obtained by multiply -1 with the range of f(x). Hence the range of g(x) is [-1, 0].

(c)  Sketching the graph :

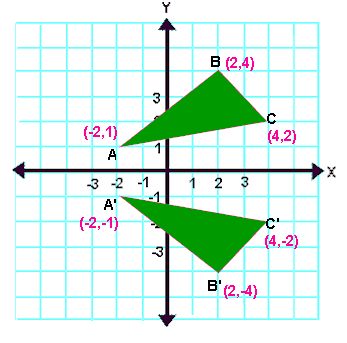
Question 2 :

Define a function h by h(x) = f(−x),

where f is the function defined by f(x) = x², with the domain of f the interval [1/2 , 1].

(a) Find the domain of h.

(b) Find the range of h.

(c) Sketch the graph of h.

Solution :

From the given question h(x)  =  f(-x), we come to know that, we have to perform reflection of y axis.

(a)  According to the definition,to get the domain of the function g(x), we have to multiply the domain of f(x) by the coefficient of 1, that is -1.

So the domain of g(x) is [-1, -1/2]

(b) Because h(x) equals f(−x), we see that the values taken on by h are the same as the values taken on by f . Thus the range of h equals the range of f , which is the interval [ 1/4 , 1].

(c)  Sketching the graph :

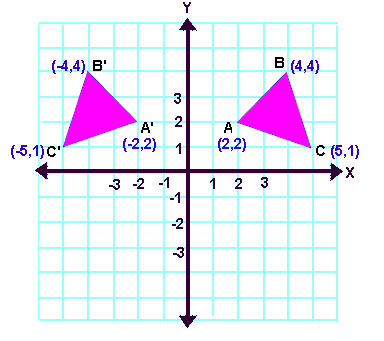
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.