REFLECTION OF SHAPES ON A GRAPH
When P(x, y) is reflected in the mirror line to become p'(x', y'), the mirror line perpendicularly bisects pp'
Thus, for every point of an object, the mirror line is perpendicularly bisects the line segment joining the point with its image.
|
Reflection on x axis |
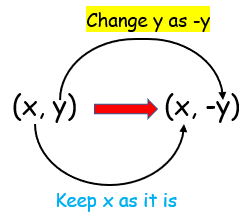 |
|
Reflection on y axis |
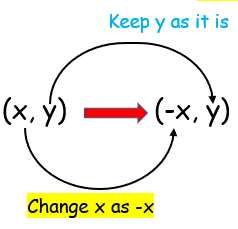 |
|
Reflection about y = x |
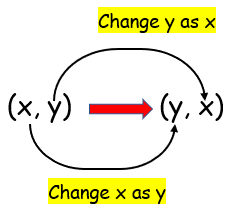 |
|
Reflection about y = -x |
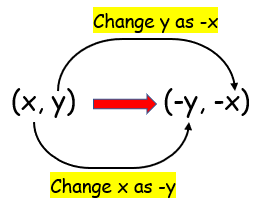 |
Example 1 :
Reflection across the line y = -x
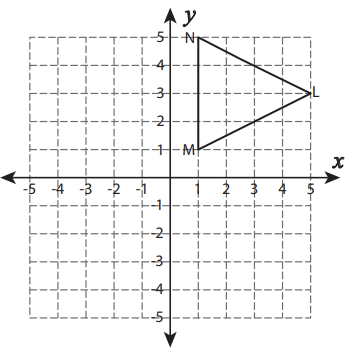
Solution :
The vertices of the given triangle are
L(5, 3), M(1, 1) and N(1, 5)
Required transformation :
Reflection about y = x
Rules to be followed :
Put x = -y and y = -x
|
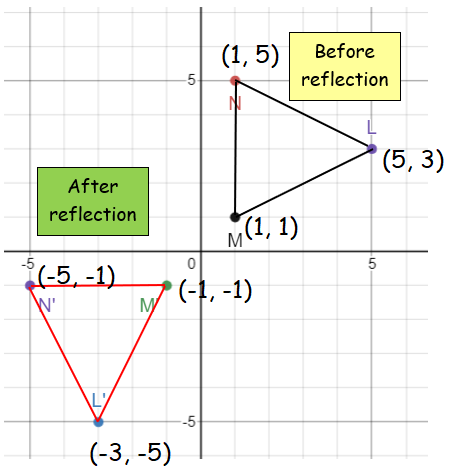
Original points L (5, 3) M (1, 1) N (1, 5) |
After reflection L' (-3, -5) M' (-1, -1) N' (-5, -1) |
Example 2 :
Reflection across the line y axis.
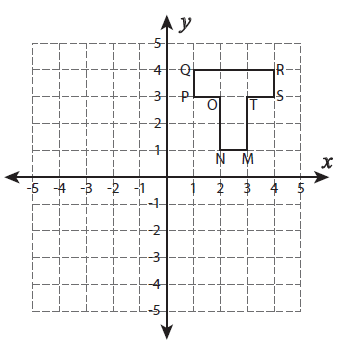
Solution :
Required transformation :
Reflection across the line y - axis.
Rules to be followed :
Put x = -x
|
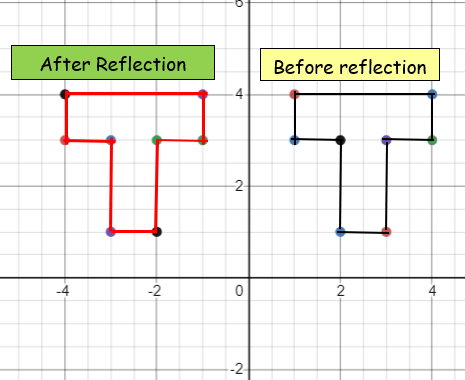
Original points P(1, 3) Q(1, 4) R(4, 4) S(4, 3) T(3, 3) O(2, 3) M(3, 1) N(2, 1) |
After Reflection P'(-1, 3) Q'(-1, 4) R'(-4, 4) S'(-4, 3) T'(-3, 3) O'(-2, 3) M'(-3, 1) N'(-2, 1) |
Example 3 :
Reflection across the line x = 3.
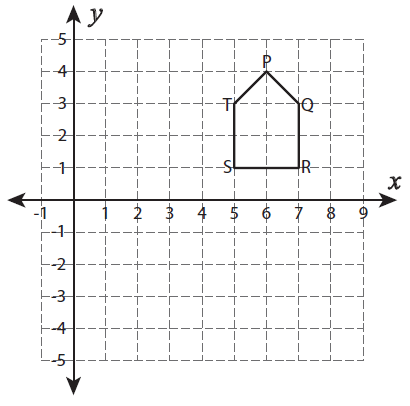
Solution :
Required transformation :
Reflection across the line x = 3
Rules to be followed :
Draw the line x = 3
Step 1 :
Calculate the distance between the vertical line and the point P.
Distance between P from the vertical line is 3 units.
Step 2 :
With the same distance plot another point in the left side of x = 3. It is named as P'.
By following the same procedure, we can mark the remaining points.
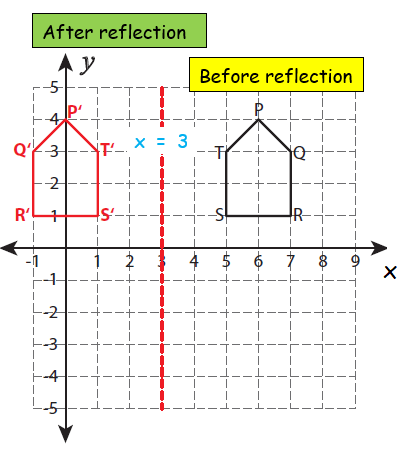
Example 4 :
Reflection across the line y = -5.
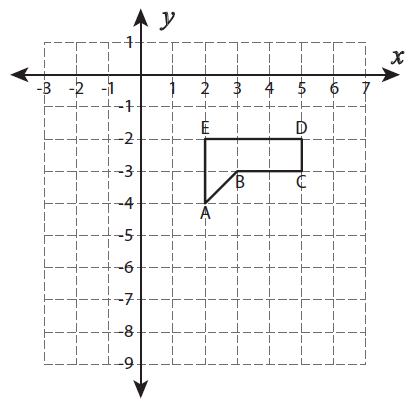
Solution :
Required transformation :
Reflection across the line y = -5
Rules to be followed :
Draw the line y = -5
Step 1 :
Calculate the distance between the horizontal line and the point A.
Distance between A from the horizontal line is 1 unit.
Step 2 :
With the same distance plot another point at the bottom of y = -5. It is named as A'.
By following the same procedure, we can mark the remaining points.
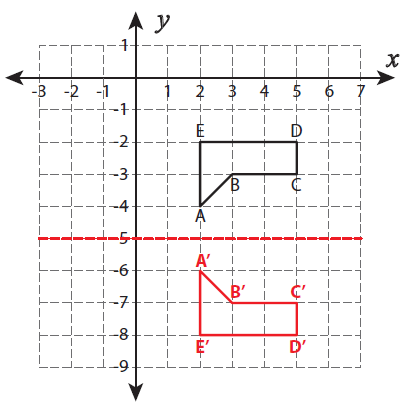
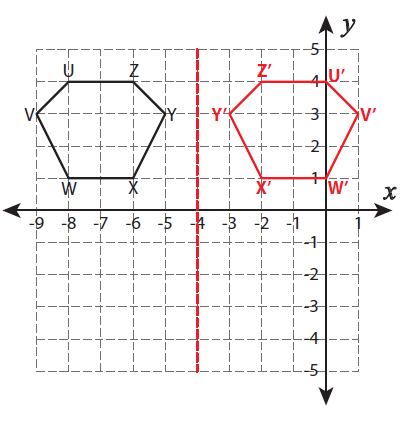
Example 5 :
Reflection across the line x = –4
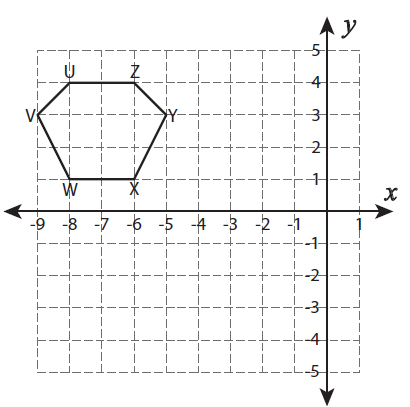
Solution :
Required transformation :
Reflection across the line x = -4
Rules to be followed :
Draw the line x = -4
Step 1 :
Calculate the distance between the vertical line and the point X.
Distance between P from the vertical line is 2 units.
Step 2 :
With the same distance plot another point to the right side of x = -4. It is named as X'.
By following the same procedure, we can mark the remaining points.
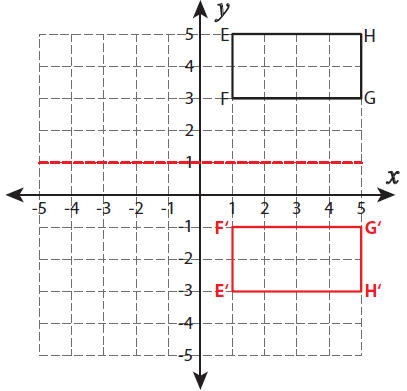
Example 6 :
Reflection across the line y = 1
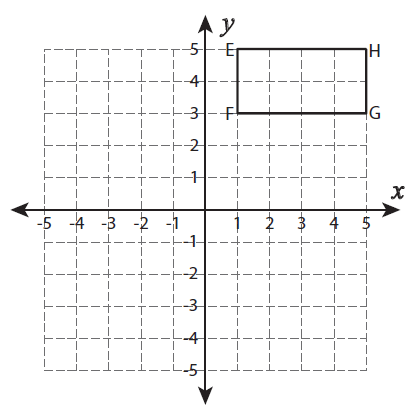
Solution :
Required transformation :
Reflection across the line y = 1
Rules to be followed :
Draw the line y = 1
Step 1 :
Calculate the distance between the horizontal line and the point F.
Distance between A from the horizontal line is 2 units.
Step 2 :
With the same distance plot another point at the bottom of y = 1. It is named as F'.
By following the same procedure, we can mark the remaining points.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
