REFLECTION TRANSLATION AND DILATION EXAMPLES

Reflection :

A reflection is the mirror image of the graph where line l is the mirror of the reflection.

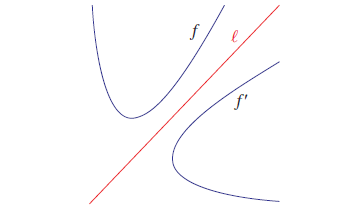
Here f' is the mirror image of f with respect to l. Every point of f has a corresponding image in f'. Some useful reflections of y = f(x) are

(i) The graph y = -f(x) is the reflection of the graph of f about the x-axis.

(ii) The graph y = f(-x) is the reflection of the graph of f about the y-axis.

(iii) The graph of y = f⁻¹(x) is the reflection of the graph of f in y = x.

Translation :

A translation of a graph is a vertical or horizontal shift of the graph that produces congruent graphs.

The graph of

y = f(x + c), c > 0 causes the shift to the left.

y = f(x − c), c > 0 causes the shift to the right.

y = f(x) + d, d > 0 causes the shift to the upward.

y = f(x) − d, d > 0 causes the shift to the downward.

Consider the functions:

(i) f(x) = |x| (ii) f(x) = |x − 1| (iii) f(x) = |x + 1|

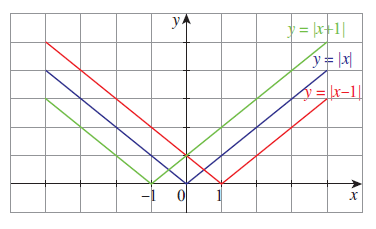
Dilation :

Dilation is also a transformation which causes the curve stretches (expands) or compresses (contracts). Multiplying a function by a positive constant vertically stretches or compresses its graph; that is, the graph moves away from x-axis or towards x-axis.

If the positive constant is greater than one, the graph moves away from the x-axis. If the positive constant is less than one, the graph moves towards the x-axis.

Consider the functions:

(i) f(x) = x² (ii) f(x) = (1/2) x² (iii) f(x) = 2x²

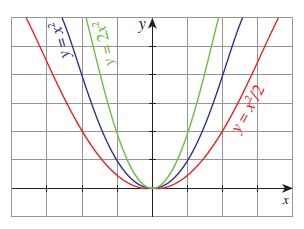
Solved Examples

Example 1 :

For the curve y  =  x³ given in the figure shown below, draw

(i)  y  =  −x³

(ii)  y  =  x³ + 1

(iii)  y  =  x³ − 1

(iv)  y  =  (x + 1)³ with the same scale.

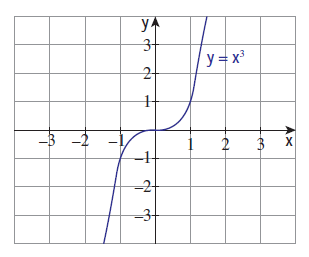
Solution :

(i)  y  =  −x³

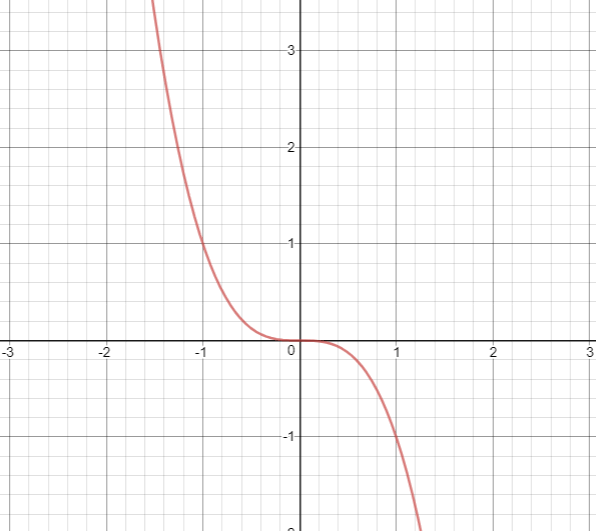
To find the graph of y = −x³, we have to use the concept reflection.

Let f(x)  =  x³

f(-x)  =  (-x)³

f(-x)  =  -x³

f(-x)  =  -f(x)

So, the reflection is about x-axis.

(ii)  y  =  x³ + 1

To graph the above function, we have to use the concept translation. That is, move the curve 1 unit upward.

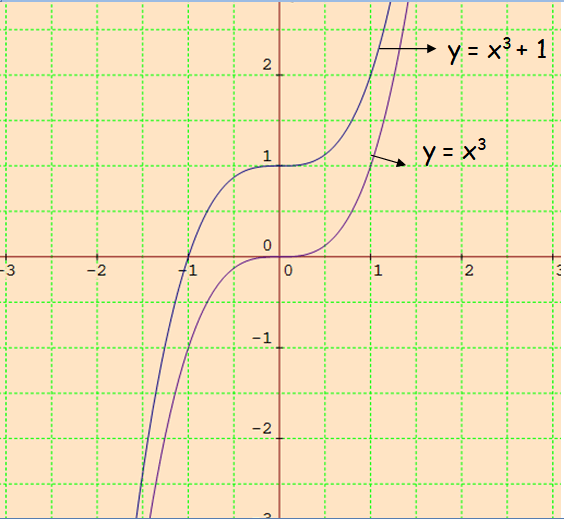
(iii)  y  =  x³ − 1 

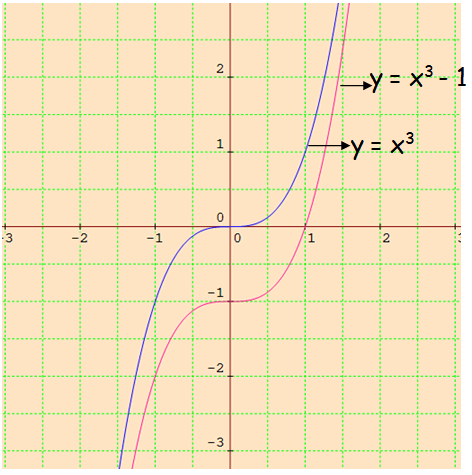
To graph the above function, we have to use the concept translation. That is, move the curve 1 unit downward.

(iv)  y  =  (x + 1)³ 

To graph the above function, we have to use the concept translation. That is, move the curve 1 unit left side.

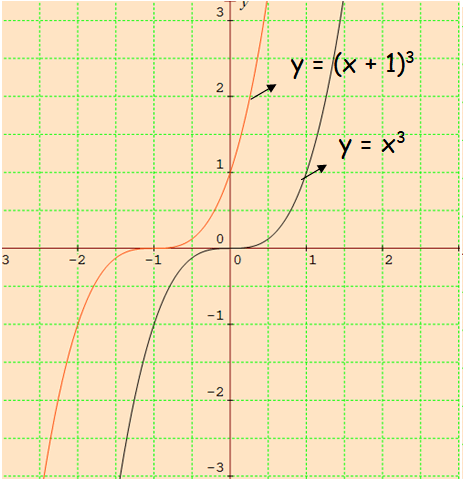
Example 2 :

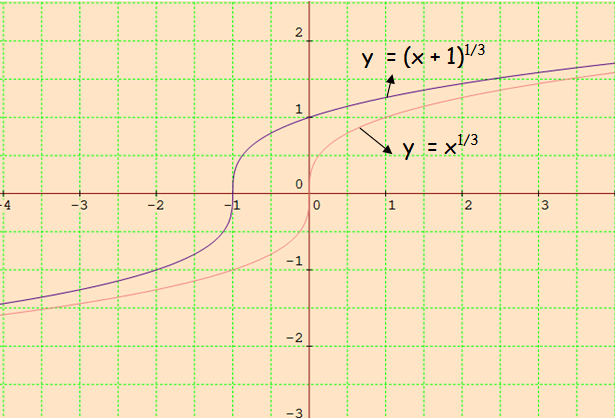
For the curve y  =  x^1/3 given in the following figure, draw

(i)  y  =  -x^1/3

(ii)  y  =  x^1/3 + 1 

(iii)  y  =  x^1/3 - 1 

(iv)  y   =  (x + 1)^1/3

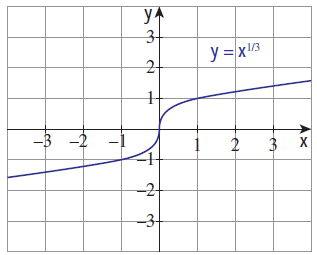
Solution :

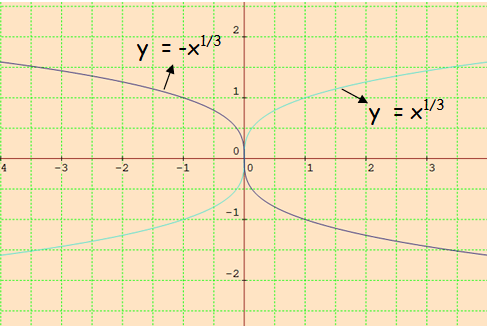
(i)  y  =  -x^1/3

Here we have negative sign in front of x^1/3

f(x)  =  x^1/3

f(-x)  =  (-x)^1/3

 f(-x)  =  -x^1/3

 f(-x)  =  -f(x)

So, the reflection is about x - axis.

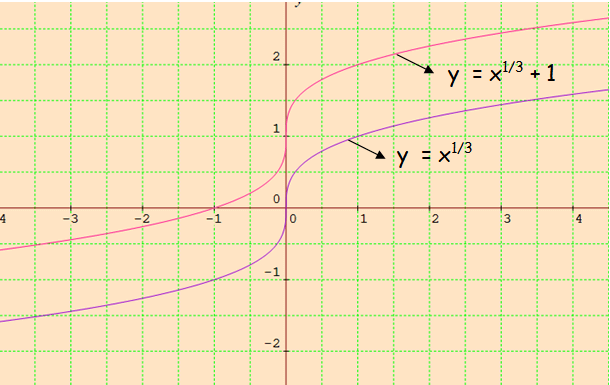
(ii) y  =  x^1/3 + 1 

Since 1 is added with the given function, we have to move the curve 1 unit upward.

(iii)  y  =  x^1/3 - 1 

Since 1 is subtracted from the given function, we have to move the curve 1 unit downward.

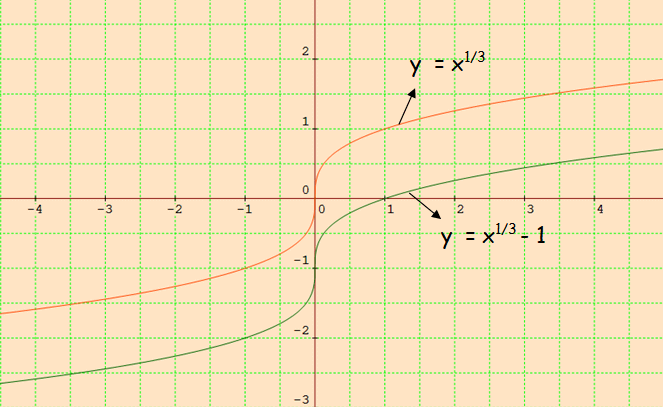
(iv)  y  =  (x + 1)^1/3

Since 1 is added to x in the given function, we have to move the curve 1 unit left side.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.