RELATIONS AND FUNCTIONS FOR GRADE 10

Question 1 :

The functions f and g are defined by f (x) = 6x + 8; g (x)  = (x - 2)/3

(i) Calculate the value of gg (1/2)

(ii) Write an expression for gf (x) in its simplest form.

Solution :

g (x)  = (x - 2)/3

g(1/2)  =  ((1/2) - 2)/3

  =  (-3/2)/3

g(1/2)   =  -1/2

gg(1/2)  =  ((-1/2) - 2)/3

=  (-5/2)/3

gg(1/2)  =  -5/6

(ii) Write an expression for gf (x) in its simplest form.

gf (x)  =  g[6x +8]

Now we have to apply 6x + 8 instead of x in g(x).

  =  [(6x + 8) - 2]/3

  =  (6x + 6)/3

  =  2x + 2  

=  2 (x + 1)

Question 2 :

Write the domain of the following real functions.

(i) f (x)  =  (2x + 1)/(x - 9)

Solution :

To find the domain, let us equate the denominator to 0

x - 9 = 0 

x  =  9

The function is defined for all real values of x except 9.

Hence the required domain is R - {9}.

(ii)  p(x)  =  -5/(4x² + 1)

Solution :

In the denominator, we have x2. For all real values of x, we get positive values. Hence the required domain is R. 

(iii)  g(x)  =  √(x - 2)

Solution :

Since the given function is in radical sign, we should not get negative answer. For that we have to apply the values grater than 2.

Hence the required domain for he given function is [2, ∞)

(iv) h(x)  =  x + 6

Solution :

For all real values of x, we get defined values of h(x). Hence the domain is R.

Question 3 :

The value of a car t years after purchase is given by 

V(t) = 28000 - 4000t dollars

a)  Find V(4)  and state what this value means.

b) Find t when V(t) = 8000 and explain what this represents.

c)  Find the original purchase price of the car.

d)  Do you think this formula is valid for all t > 0 ?

Solution :

V(t) = 28000 - 4000t dollars

a)  V(4) = 28000 - 4000(4)

= 28000 - 16000

= 12000

After 4 years, the value of the car is 12000.

b)  V(t) = 8000

28000 - 4000t = 8000

4000 t = 28000 - 8000

4000 t = 20000

t = 20000/4000

t = 5

c) When t = 0, the original price V(0)

V(0) = 28000 - 4000(0)

V(0) = 28000 - 0

= 28000

So, the original price is $28000.

d)  Here t represents the number of years after purchase. Then the starting value of t must be 0. So, the given formula is valid only for t > 0.

Question 4 :

Sketch the graph of y = f(x), where f(x) = 2x - 1 on the domain {x |-3 ≤ x ≤ 1}. State the range of this function.

Solution :

f(x) = 2x - 1

Considering the function f(x), it is a linear function. The graph must be a straight line and raising line since the slope is positive.

Comparing the given linear function with y = mx + b, we get

Slope (m) = 2 and y-intercept (b) = -1

(-3, -7) (-2, -5) (-1, -3) (0, -1) (1, 1)

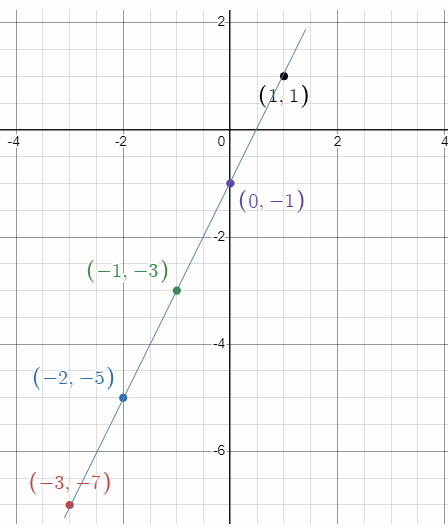
Question 5 :

The graph of the function is given below

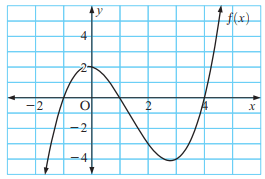
a) find f(2)

b) Estimate x, when f(x) = -1

Solution :

a)  We have to evaluate when x = 2, by drawing the vertical line.

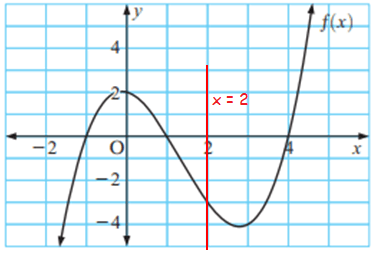
y = -3

b) when y = -1, x = 0

Question 6 :

Let f(x) = x² + 2x and g(x) = x - 2. Find in simplest form

a) f(g(2)) and f(g(x))

b) g(f(2)) and g(f(x))

Solution :

a) 

f(x) = x² + 2x and g(x) = x - 2.

f(g(x)) = f[x - 2]

Applying x - 2 as x in f(x), we get

= (x - 2)² + 2(x - 2)

= x² - 4x + 4 + 2x - 4

f(g(x)) = x² - 2x

Applying x = 2

f(g(2)) = 2² - 2(2)

= 4 - 4

= 0

b)

f(x) = x² + 2x and g(x) = x - 2.

g(f(x)) = g[x² + 2x]

Applying x² + 2x as x in g(x), we get

g(f(x)) = x² + 2x - 2

Applying x = 2

g(f(2)) = 2² + 2(2) - 2

= 4 + 4 - 2

= -2

Question 7 :

If f(x) = 3x + 1 and g(x) = 2x - 3, find x when g(f(x)) = 17

Solution :

f(x) = 3x + 1 and g(x) = 2x - 3

g(f(x)) = g[3x + 1]

Applying the value of f(x) as x in the function g(x).

g[3x + 1] = 2(3x + 1) - 3

= 6x + 2 - 3

g(f(x)) = g[3x + 1]= 6x - 1

g(f(x)) = 17

6x - 1 = 17

6x = 17 + 1

6x = 18

x = 18/6

x = 3

So, the value of x is 3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.