RELATIONS AND FUNCTIONS PRACTICE TEST

To find questions from 1 to 4, please visit the page "Practice Worksheet Relations and Functions with Answers"

Question 5 :

Find the domain of the function f(x) =

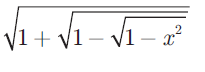
Solution :

Let t = √(1 - √(1 - x²))

f(x)  =  √(1 - t)

1 - t ≥ 0

t ≤ 1

By applying the value of t, we get

√(1 - √(1 - x²)) ≤ 1

1 - √(1 - x²)) ≤ 1

Subtracting 1 through out the equation,

- √(1 - x²)) ≤ 0

√(1 - x²)) ≥0

Taking squares on both sides,

(1 - x²)  ≥ 0

 - x² ≥ -1

x ≤ 1

Hence the domain is x ∈ [-1, 1]

Question 6 :

If f (x) = x² , g(x) = 3x and h(x) = x −2 , Prove that (f ∘ g) ∘ h = f ∘ (g ∘ h) .

Solution :

L.H.S :

R.H.S :

Hence proved.

Question 7 :

Let A = {1, 2} and B = {1, 2, 3, 4} , C = {5, 6} and D = {5, 6 ,7, 8} . Verify whether A × C is a subset of B × D?

Solution :

A = {1, 2} and C = {5, 6}

A x C  =  {(1, 5) (1, 6) (2, 5) (2, 6)}  ----(1)

B = {1, 2, 3, 4} and D = {5, 6 ,7, 8}

B x D  =  { (1, 5) (1, 6) (1, 7) (1, 8) (2, 5) (2, 6) (2, 7) (2, 8) (3, 5) (3, 6) (3, 7) (3, 8) (4, 5) (4, 6) (4, 7) (4, 8) }

Hence A x C is the subset of B x D.

Question 8 :

If f(x)  =  (x - 1)/(x + 1), x ≠ 1 show that f(f(x))  =  -1/x, provided x ≠ 0

Solution :

f(x)  =  (x - 1)/(x + 1) (Given)

f(f(x))  =  

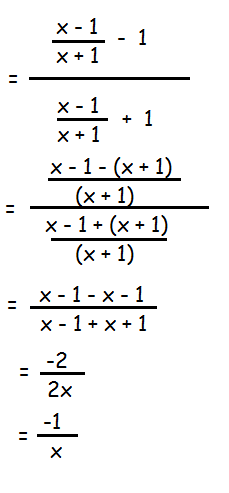
Hence proved.

Question 9 :

If the universal set E = {x : x is a positive integer < 25}, A = {2, 6, 8, 14, 22}, B = {4, 8, 10, 14} Prove that (A n B)' = A' U B'

Solution :

E = {1, 2, 3, 4, 5, ............ 25}, A = {2, 6, 8, 14, 22}, B = {4, 8, 10, 14}

A n B = {8, 14}

(A n B)' = {1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25} -----(1)

A' = {1, 3, 4, 5, 7, 9, 10, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 23, 24, 25}

B' = {1, 2, 3, 5, 6, 7, 9, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25}

A'UB' =  {1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25} -----(2)

(1) = (2)

Hence it is proved.

Question 10 :

A survey shows that 74% of the Indian like grapes, whereas 68% like bananas. What percentage of the Indian like both grapes and bananas if everybody likes wither fruit ?

a)  42%    b)  26%     c)  58%       d)  62%

Solution :

Let A be grapes and B be banana

Total number of people surveyed = 100

n(A) = 74

n(B) = 68

Let x be the number of people who likes both Grapes and Bananas.

n(AnB) = x

n(AuB) = n(A) + n(B) - n(AnB)

100 = 74 + 68 - x

100 = 142 - x

x = 142 - 100

x = 42

So, 42% of people who likes both grapes and bananas.

Question 11 :

If f(x) : N->R is a function defined as f(x) = 4x + 3 for all x belongs to N, the f^-1(x) is

Solution :

f(x) = 4x + 3

Let y = 4x + 3

Solve for x,

y - 3 = 4x

x = (y - 3) / 4

Replace x by f^-1(x) and y by x.

f^-1(x) = (x - 3) / 4

Question 12 :

The number of subsets of the set {0, 1, 2, 3} is

Solution :

Let A = {0, 1, 2, 3}

Number of elements in the set A, that is n(A) = 4

Number of subsets = 2ⁿ

= 2⁴

= 16

So, the number of subsets of the set A is 16.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.