RELATIONSHIP BETWEEN DOMAIN AND RANGE OF A FUNCTION AND ITS INVERSE

In this section, you will learn the relationship between domain and range of a function and its inverse.  

Practice Questions

Question 1 :

For each of the functions f given in 

(a) Find the domain of f  (b) Find the range of f

(c) Find a formula for f⁻¹  (d) Find the domain of f⁻¹

(e) Find the range of f⁻¹

f(x) = 3x + 5

Answer :

(a)  For any real values of x  the function will not be undefined. So, the domain is a set of all real numbers.

(b)  Range of f(x) is also a set of all real numbers.

(c)  In order to find the inverse function, first we have to prove the given function is one to one.

Every different values of x is associated with unique values of f(x). So it is one to one function

y  =  3x + 5

3x  =  y - 5

x  =  (y - 5)/3

f^-1(y)  =  (y - 5)/3

(d) Find the domain of f⁻¹

Range of f  =  Domain of f^-1

So, the domain of f^-1 is a set of all real numbers.

(d) Find the range of f⁻¹

Domain of f  =  Range of f^-1

So, the range of f^-1 is a set of all real numbers.

Question 2 :

Suppose f is the function whose domain is the set of real numbers, with f defined on this domain by the formula f(x) = |x + 6|. Explain why f is not a one-to-one function

Answer :

We have absolute sign for the given function.

For all positive and negative values of x, it must be associated with positive values only. For example,

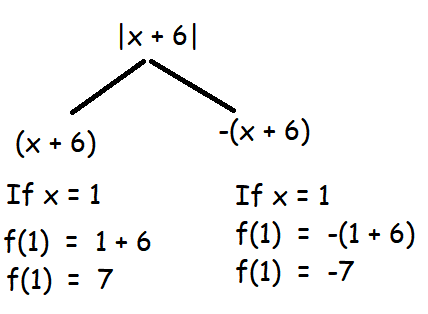
For 1, we have two different images. Hence it is not one function.

Question 3 :

Consider the function h whose domain is the interval [−4, 4], with h defined on this domain by the formula

h(x) = (2 + x)²

Does h have an inverse? If so, find it, along with its domain and range. If not, explain why not.

Answer :

In order to prove the given is one to one, first we have to show it as one to one function.

Like this, for every different values of h(x) is associated with different values. Hence it is one to one.

Inverse of h(x) :

y = (2 + x)²

√y =  (2 + x)

x  =  √y - 2

f^-1(y)  =  √y - 2

Range of f  =  Domain of f^-1

Domain of f^-1  =  [0, 36]

Domain of f  =  Range of f^-1

Range of f^-1  =  [-4, 4]

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.