RELATIONSHIP BETWEEN HCF AND LCM

Let us find the highest common factor (HCF) and the least common multiple (LCM) of 36 and 48.

First, find the factors of 36 and 48 using division method.

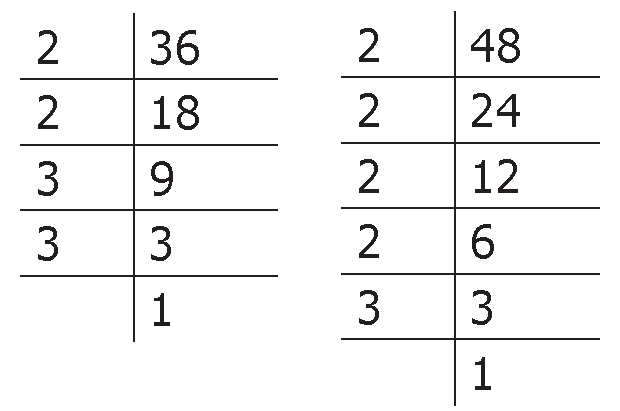
36  =  2 x 2 x 3 x 3

48  =  2 x 2 x 2 x 2 x 3

HCF (36, 48)  =  2 x 2 x 3  =  12

LCM (36, 48)  =  2 x 2 x 3 x 2 x 2 x 3  =  144

HCF x LCM  =  12 x 144  =  1728 -----(1)

And also, product of the two numbers 36 and 48 : 

36 x 48  =  144 x 12  =  1728 -----(2)

From (1) and (2), we find that,

Product of two given numbers  =  HCF x LCM

In general, for any 2 numbers 'a' and 'b',

a x b  =  HCF (a, b) x LCM (a, b)

So, from the above explanations we conclude that the  product of highest common factor (HCF) and lowest common multiple (LCM) of two numbers is equal to the product of two numbers. 

HCF x LCM  =  First Number x Second Number

HCF  =  (First Number x Second Number) / LCM

LCM  =  (First Number x Second Number) / HCF

Example 1 : 

The LCM of two numbers is 432 and their HCF is 36. If one of the numbers is 108, then find the other number.

Solution : 

Let x be the other number. 

We know that,

Product of the two numbers  =  LCM x HCF

Then, 

108(x)  =  432 x 36

Divide each side by 108.

x  =  (432 x 36) / 108

x  =  144

The other number is 144.

Example 2 : 

Two numbers are in the ratio 2 : 3 and their HCF is 13. Find the LCM of those two numbers. 

Solution : 

Because the two numbers are in the ratio 2 : 3, the numbers can be assumed as 2x and 3x.

HCF (2x, 3x)  =  x

But, it is given that the HCF is 13.

Then, 

x  =  5

Substitute x = 13 in 2x and 3x.

2x  =  2(13)  =  26

3x  =  3(13)  =  39

So, the two numbers are 26 and 36.

We know that,

HCF x LCM  =  Product of the two numbers

Substitute.

13x LCM  =  26 x 39

Divide each side by 13.

LCM  =  (26 x 39) / 13

LCM  =  78

Example 3 : 

The LCM of two co-prime numbers is 5005. If one of the numbers is 65, then find the other number.

Solution : 

Let x be the other number.

We know that,

Product of the two numbers  =  LCM x HCF

As the HCF of co-primes is 1,

65(x)  =  5005 ⋅ 1

65x  =  5005

Divide each side by 65.

x  =  77

The other number is 77.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.