REPRESENT THE GIVEN INTERVAL ON THE NUMBER LINE

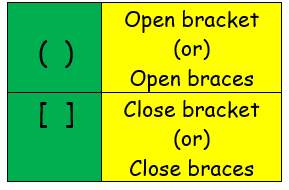
An open interval does not include its endpoints, and is enclosed in parentheses.

A closed interval includes its endpoints, and is enclosed in square brackets.

An interval is considered bounded if both endpoints are real numbers. An interval is unbounded if both endpoints are not real numbers.

Example 1 :

Graph the given interval on the number line.

(i)  (-∞, 5)

(ii)  [-2, 2)

(iii)  [-1, ∞)

(iv)  [-3, 0]

Solution :

(i)  (-∞, 5)

Converting the given interval notation as -inequality, we get

-∞ < x < 5

The possible values of x are greater than infinity but less than 5. (should not include 5).

(ii)  [-2, 2)

Converting the given interval notation as inequality, we get

-2 ≤ x < 2

The possible values of x are greater than or equal to -2 and less than 2.

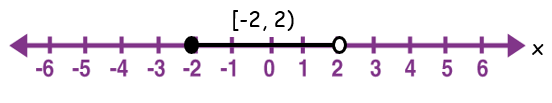
(iii)  [-1, ∞)

Converting the given interval notation as inequality, we get

-1 ≤ x < ∞

The possible values of x are greater than or equal to -1 and less than infinity.

(iv)  [-3, 0]

Converting the given interval notation as inequality, we get

-3 ≤ x ≤ 0

The possible values of x are greater than or equal to -3 and less than or equal to 0.

Example 2 :

Describe and graph the interval of real numbers.

(i)  x ≤ 2

Solution :

Interval notation of given inequality is (-∞, 2].

The values which are less than or equal to 2 can be considered as solution.

By shading the possible solutions on the number line, we get

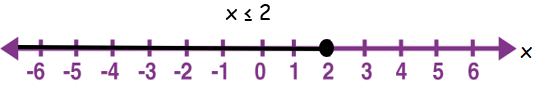
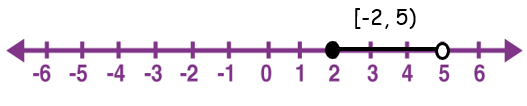
(ii)  -2 ≤ x < 5

Solution :

Interval notation of given inequality is [-2, 5).

The values which are greater than or equal to -2 and less than 5 can be considered as solution.

By shading the possible solutions on the number line, we get

(iii)  (-∞, 6)

Solution :

By writing the given interval using inequality, we get

-∞ < x < 6

The values which are greater than -infinity and less than 6 can be considered as solution.

By shading the possible solutions on the number line, we get

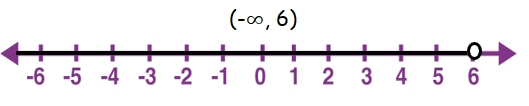
(iv)  [-3, 3]

Solution :

By writing the given interval using inequality, we get

-3≤< x ≤ 3

The values which are greater than or equal to -3 and less than or equal to 3.

By shading the possible solutions on the number line, we get

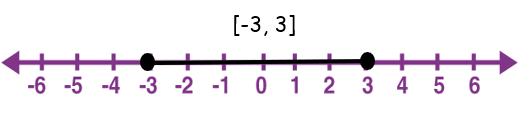
Example 3 :

Frozen chickens will be sold by a major chain of supermarkets only if their weight is at least 1.2 kg and not more than 3.4 kg,

(i) Represent this information on the number line

ii)  Write the interval to describe the region which you have marked

Solution :

a)

• At least 1.2 kg, then x ≥ 1.2
• Not more than 3.4, then x ≤ 3.4

b)  Representing it as interval notation.

1.2 ≤ x ≤ 3.4

(i)  Use an inequality symbol to write each statement.

(ii) Write the solution as interval notation.

Example 4 :

2x is between −2 and 6, including −2 and excluding 6

Solution :

i)  -2 ≤ 2x ≤ 6

Dividing by 2 throughout the equation

-1 ≤ x ≤ 3

(ii)  Writing interval notation :

[-1, 3]

Example 5 :

x + 1 is between −5 and 11, excluding −5 and including 11

Solution :

i)  -5 ≤ x + 1 ≤ 11

Subtracting 1 throughout the inequality, we get

-5 - 1  ≤ x + 1 - 1 ≤ 11 - 1

-6 ≤ x ≤ 10

(ii)  Writing interval notation :

[-6, 10]

Example 6 :

Chris runs a barber shop. It costs him $20 per day to cover his expenses and the charges $4 for every hair cut. 

a) Explain why his profit for any day is (4x - 20), where x is the number of haircuts in that day.

b)  He hopes to make atleast $50 profit per day, but does not intend to make more than $120 profit 

b) Write down an inequality to describe this situation.

Solution :

a)  Profit per day = 4x - 20

Here x is the number of haircuts in that day.

4x is the amount he is earning for haircut. Since he spends 20, we subtract it. 4x - 20 is the profit.

50 < 4x - 20 < 120

To isolate x, we have to add 20 throughout the inequality. 

50 + 20 < 4x < 120

70 < 4x < 120

Dividing by 4, we get

70/4 < x < 120/4

17.5 < x < 30

So, number of haircuts should be made is in between 18 to 30.

Example 7 :

A man finds that his electricity bill varies between £50 and £90.

(a) If C represents the size of his bill, write down an inequality involving C.

The bill is made up of a standing charge of £10 and a cost of 10 pence per kilowatt hour of electricity.

(b) If n is the number of kilowatt hours used, write down a formula for C in terms of n. 

Using your formula, write down an inequality involving n and solve this inequality.

Solution :

a) Varies between 50 and 90

50 < C < 90

Standing charge = £10

Let n be the number of hours.

cost per kilowatt = 0.10n

C = 0.10n + 10

50 < 0.10n + 10 < 90

Subtracting 10 on everywhere

50 - 10 < 0.10n < 90 - 10

40 < 0.10n < 80

Dividing by 0.10, we get

40/0.10 < n < 80/0.10

400 < n < 800

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.