REPRESENTATION OF FUNCTION AND TYPES OF FUNCTIONS WORKSHEET

(1)  Determine whether the graph given below represent functions. Give reason for your answers concerning each graph.

(i)	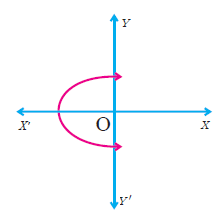(ii)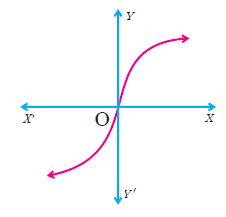
(iii)	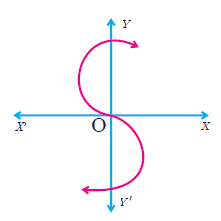(iv)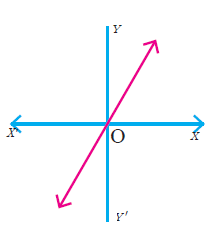

Solution

(2)  Let f : A -> B be a function defined by f (x) =  (x/2) - 1 where A = {2, 4, 6, 10, 12}, B = {0, 1, 2, 4, 5, 9} .

Represent f by 

(i) set of ordered pairs; (ii) a table; (iii) an arrow diagram; (iv) a graph 

Solution

(3)  Represent the function f = {(1, 2),(2, 2),(3, 2),(4, 3),(5, 4)} through (i) an arrow diagram (ii) a table form (iii) a graph       Solution

(4)  Show that the function f : N -> N defined by f (x) = 2x – 1 is one-one but not onto     Solution

(5)  Show that the function f : N -> N defined by f (m) = m² + m + 3 is one-one function.      Solution

(6)  Let A = {1, 2, 3, 4} and B = N . Let f : A -> B be defined by f (x) = x³ then, (i) find the range of f (ii) identify the type of function      Solution

(7)  In each of the following cases state whether the function is bijective or not. Justify your answer.

(i) f : R -> R defined by f (x) = 2x +1

(ii) f : R -> R defined by f (x) = 3 – 4x²    

Solution

(8)  Let A = {−1, 1}and B = {0, 2} . If the function f : A -> B defined by f(x) = ax + b is an onto function? Find a and b.

Solution

(9)  If the function f is defined by

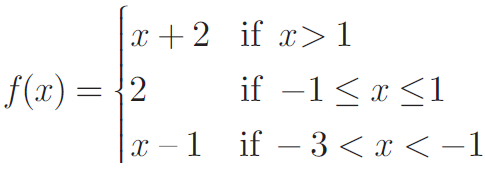
find the values of

(i) f (3) (ii) f (0) (iii) f (−1.5) (iv) f (2)+ f (−2)     Solution

(10)  A function f : [−5,9] -> R is defined as follows:

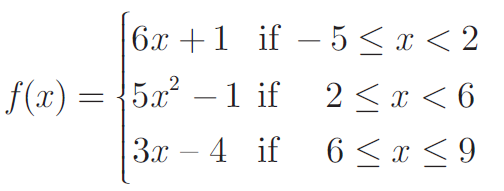
Find (i) f (−3) + f (2) (ii) f (7) - f (1) (iii) 2f (4) + f (8)

(iv)  [2f(-2) - f(6)] / [f(4) + f(-2)]     Solution

(11)  The distance S an object travels under the influence of gravity in time t seconds is given by

S(t) = (1/2) gt² + at + b

where, (g is the acceleration due to gravity), a, b are [constants. Check if the function S(t) is one-one.   

Solution

(12)  The function ‘t’ which maps temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by

t(C) = F where F = (9/5) C + 32 .

Find, (i) t(0)   (ii) t(28)   (iii) t(-10)

(iv) the value of C when t (C)  =  212

(v) the temperature when the Celsius value is equal to the Farenheit value.     Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.