REPRESENTING LINEAR NON PROPORTIONAL RELATIONSHIPS WORKSHEET

Problem 1 :

The diameter of a Douglas fir tree is currently 10 inches when it is measured at chest height. After 50 years, the diameter is expected to increase by an average growth rate of 2/5 inch per year. The equation y=(2/5)x+10  gives y, the diameter of the tree in inches, after x years. Draw a graph of the equation. Describe the relationship.

Problem 2 :

The equation y = x/6  gives y, the weight of moon in pounds for the weight of earth, x in pounds.  Draw a graph of the equation. Describe the relationship.

Problem 3 :

The entrance fee for Mountain World theme park is $20. Visitors purchase additional $2 tickets for rides, games, and food. The equation y = 2x + 20 gives the total cost, y, to visit the park, including purchasing x tickets. Explain  why the relationship between number of tickets and total cost is not proportional.

1. Answer :

Step 1 :

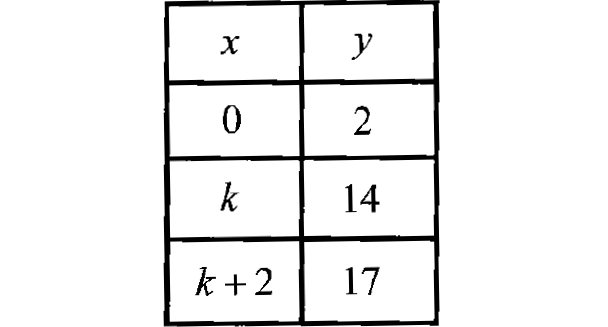
Make a table. Choose several values for x that make sense in context. To make calculations easier, choose multiples of 10.

Step 2 :

Plot ordered pairs from the information in the table. Then draw a line connecting the points to represent all the possible solutions.

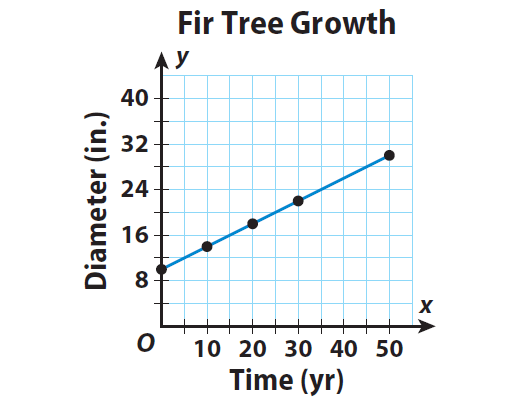
Step 3 :

The relationship is linear but non proportional. The graph is a line but it does not go through the origin.

2. Answer :

Step 1 :

Make a table. Choose several values for x that make sense in context. To make calculations easier, choose multiples of 6.

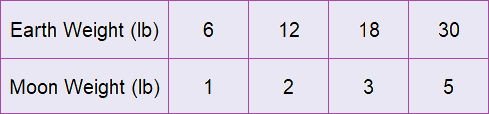
Step 2 :

Plot ordered pairs from the information in the table. Then draw a line connecting the points to represent all the possible solutions.

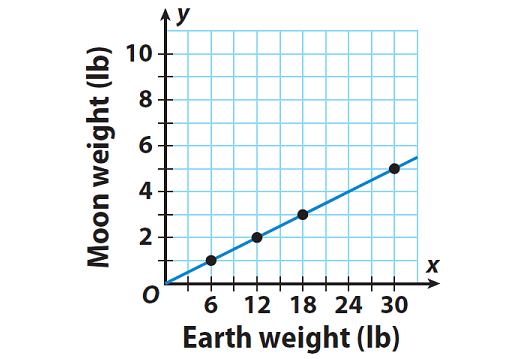
Step 3 :

The relationship is linear and also proportional. Because the graph is a line and also it goes through the origin.

3. Answer :

Step 1 :

Choose several values for x that make sense in context.

Step 2 :

Plot the ordered pairs from the table. Describe the shape of the graph.

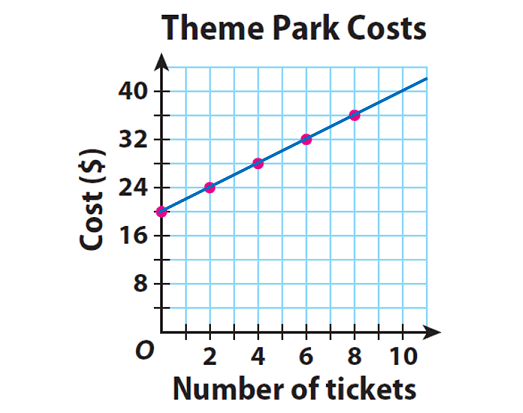
Step 3 :

In the above graph, the points lie on a line. But the line does not pass through the origin. So, the relationship between number of tickets and total cost is not proportional.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.