RHOMBUSES RECTANGLES AND SQUARES WORKSHEET

Question 1 :

Decide whether the statement given below is always, sometimes or never true.

"A rhombus is a rectangle"

Question 2 :

Decide whether the statement given below is always, sometimes or never true.

"A parallelogram is a rectangle"

Question 3 :

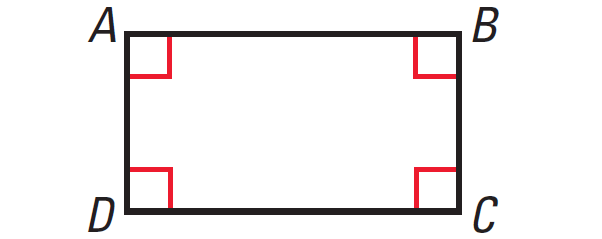
ABCD is a rectangle. What else do you know about ABCD?

Question 4 :

In the diagram at the right, PQRS is a rhombus. What is the value of y?

Question 5 :

Prove that the diagonals of a rhombus are perpendicular.

1. Answer :

"A rhombus is a rectangle"

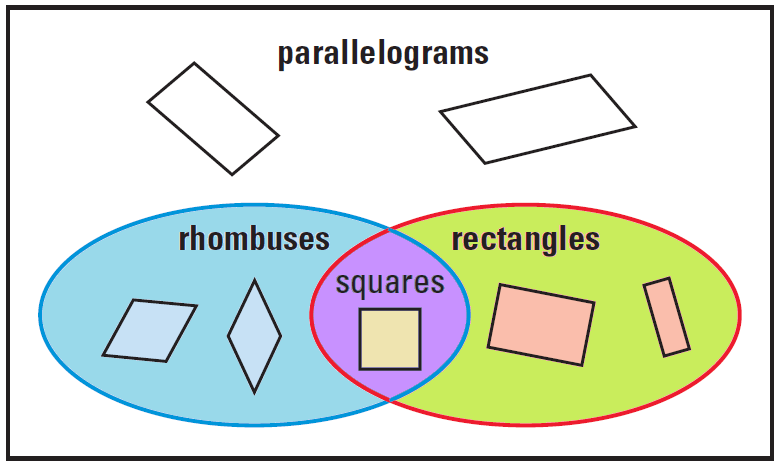
The statement is sometimes true.

In the Venn diagram above, the regions for rhombuses and rectangles overlap. If the rhombus is a square, it is a rectangle.

2. Answer :

"A parallelogram is a rectangle"

The statement is sometimes true. Some parallelograms are rectangles.

In the Venn diagram above, we can see that some of the shapes in the parallelogram box are in the region for rectangles, but many aren’t.

3. Answer :

Because ABCD is a rectangle, it has four right angles by the definition. The definition also states that rectangles are parallelograms.

So, ABCD has all the properties of a parallelogram :

• Opposite sides are parallel and congruent.

• Opposite angles are congruent and consecutive angles are supplementary.

• Diagonals bisect each other.

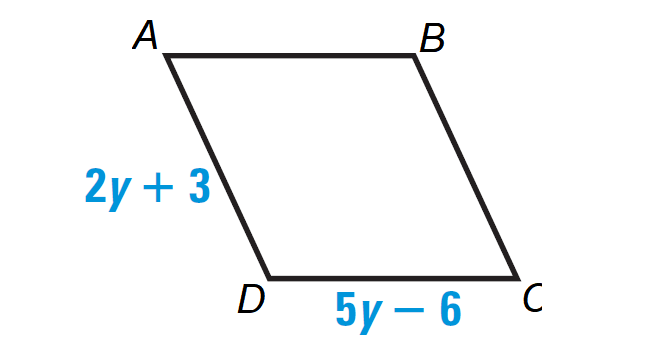
4. Answer :

All four sides of a rhombus are congruent, so we have

RS = PS

Substitute RS = 5y - 6 and PS = 2y + 3.

5y - 6 = 2y + 3

Add 6 to both sides.

5y = 2y + 9

Subtract 2y from

3y = 9

Divide both sides by 3.

y = 3

5. Answer :

Let us consider the rhombus PQRS as shown below.

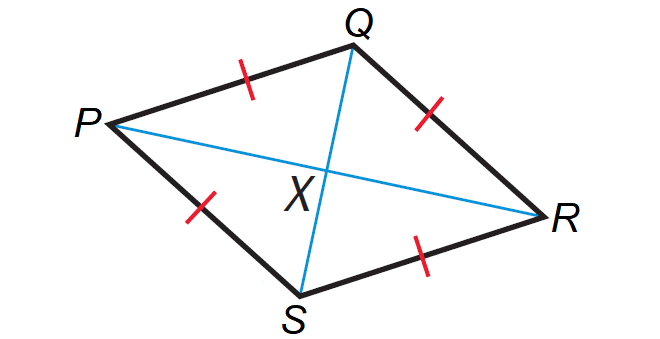
In the rhombus PQRS above, we have to prove

PR ⊥ QS

PQRS is a rhombus, so we have

PQ ≅ QR

Because the rhombus PQRS is also a parallelogram, its diagonals bisect each other.

So, we have

PX ≅ RX

PQ ≅ QR

Using SSS postulate, we have

ΔPXQ ≅ ΔRXQ

So, we have

∠PXQ ≅ ∠RXQ ----> ∠PXQ = ∠RXQ

Because ∠PXQ, ∠RXQ form a linear pair and ∠PXQ = ∠RXQ, we have

∠PXQ = ∠RXQ = 90°

Hence, we have

PR ⊥ QS

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.