ROLLES THEOREM

Example 1 :

Using Rolle's theorem find the values of c.

f(x)  =  x²-4x+3 ,  1 ≤ x ≤ 3

Solution :

(i) f (x) is continuous on [1, 3].

(ii) f(x) is differentiable (1, 3).

(iii) f(1)  =  f(3).

All conditions are satisfied.

f'(c)  =  2x-4

To find that particular point we need to set f'(c)  =  0.

2c-4  =  0

c  =  2

So, c is 2.

Example 2 :

Using Rolle's theorem find the values of c.

f(x)  =  sin² x ,   0 ≤ x ≤ Π

Solution :

(i) f (x) is continuous on [0 ,Π].

(ii) f(x) is differentiable (0,Π).

f(0)  =  sin²(0)  ==> 0

f(Π)  =  sin² (Π)  ==>  0

f(0)  =   f(Π). All conditions are satisfied.

f'(x)  =  2sinx cos x

=  sin 2x 

f'(c)  =  sin 2c 

To find that particular point we need to set f'(c)  =  0

sin 2c  =  0

2c  =  sin^-1 (0)

2c  =  0, Π, 2 Π, 3 Π , .............

c  =  Π/2∊  0 ≤ x ≤ Π

Example 3 :

Using Rolle's theorem find the points on the curve

y  =  x²+1,   - 2 ≤ x ≤ 2

where the tangent is parallel to x - axis.

Solution :

If f(x) be a real valued function that satisfies the following three conditions.

1)  f(x) is defined and continuous on [-2, 2] 

2)  f(x) is differentiable on interval (-2,2).

y  =  x²+1 

f(-2)  =  (-2)² + 1

f(-2)  = 5

f(2)  =  2²+1

f(2)  =  5

f(-2)  =  f(2)

from this we come to know that the given function satisfies all the conditions of Rolle's theorem.

c ∈ (-2, 2)

we can find the value of c by using the condition

f'(c)  =  0

f(x)  =  x² + 1

f'(x)  =  2x

f'(c)  =  2c

f'(c)  =  0

2c  =  0  

 c  =  0

f (0) = 0² + 1  ==>  1

Therefore the required point on the curve is (0, 1).

Example 4 :

Skater Sully is riding a skateboard back and forth on a street that runs north/south. The twice-differentiable function 𝑆 models Sully’s position on the street, measured by how many meters north he is from his starting point, at time 𝑡, measured in seconds from the start of his ride. The table below gives values of 𝑆𝑡 at selected times 𝑡.

a) For 0 ≤ 𝑡 ≤ 20, must there be a time 𝑡 when Sully is 2 meters south of his starting point? Justify your answer.

b) For 30 ≤ 𝑡 ≤ 60, must there be a time 𝑡 when Sully’s velocity is 1.1 meters per second? Justify your answer

Solution :

a) Since the given function is differentiable, it must be continuous function

S(0) = 0 and S(20) = -5

According to intermediate value theorem since it satisfies the first two conditions.

There must be a value -2 in between the interval 0 to -5.

b)  S(30) = 7, S(60) = 40

Using mean value theorem,

= S(60) - S(30) / (60 - 30)

= (40 - 7) / (60 - 30)

= 33/30

= 1.1 meters per second.

Example 5 :

A hot air balloon is launched into the air with a human pilot. The twice-differentiable function ℎ models the balloon’s height, measured in feet, at time 𝑡, measured in minutes. The table below gives values of ℎ𝑡 at selected times 𝑡.

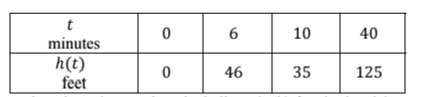
For 6 ≤ 𝑡 ≤ 10, must there be a time 𝑡 when the balloon is 50 feet in the air? Justify your answer.

b) For 10 ≤ 𝑡 ≤ 40, must there be a time 𝑡 when the balloon’s velocity is 3 feet per second?

Solution :

a)  𝒉(𝟔) = 𝟒𝟔 and 𝒉(𝟏𝟎) = 𝟑𝟓. No, the IVT does not guarantee a height of 50.

b) 𝒉(𝒕) is differentiable and

= (𝟏𝟐𝟓 - 𝟑𝟓)/(𝟒𝟎 - 𝟏𝟎)

= 𝟗𝟎/𝟑𝟎

= 3

Yes. According to the Mean value theorem, there must be a value 𝒄 where 𝟏𝟎 ≤ 𝒄 ≤ 𝟒𝟎 and 𝒉'(𝒄) = 𝟑.

Example 6 :

A particle moves along the x-axis so that its position at any time t ≥ 0 is given by x(t) = t³ - 3t² + t + 1. For what values of t, 0 ≤ t ≤ 2 is the particle's instantaneous velocity the same as its average velocity on the closed interval [0, 2]

Solution :

Average velocity = [x(2) - x(0)] / (2 - 0) ----(1)

x(t) = t³ - 3t² + t + 1

Applying these values in (1), we get

= (-1 - 1) / 2

= -2/2

= -1

Instantaneous velocity : 

x'(t) = 3t² - 3(2t) + 1 + 0

-1 = 3t² - 6t + 1

3t² - 6t + 2 = 0

Solving this quadratic equation,

a = 3, b = -6 and c = 2

b² - 4ac = (-6)² - 4(3)(2)

= 36 - 24

= 12

= (-b ± √b² - 4ac)/2a

= (6 ±√12)/2(3)

= 6 ± 2√3)/6

= (3 ±√3)/2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.