ROTATION TRANSFORMATION IN GEOMETRY

Rotation transformation is one of the four types of transformations in geometry.

We can use the following rules to find the image after 90°, 180°, 270° clockwise and  counterclockwise rotation. 

Rules on Finding Rotated Image

90° Rotation (clock wise)

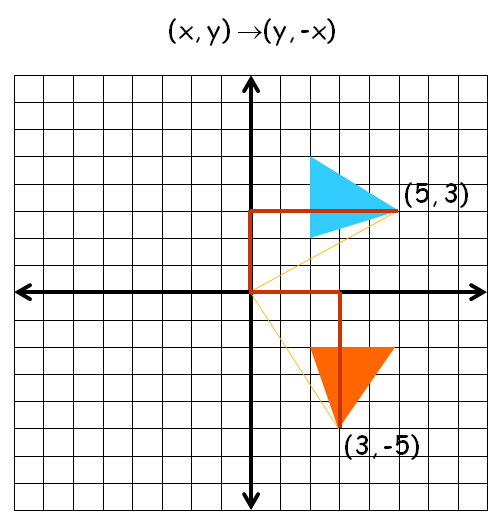
90° Rotation (counter clock wise)

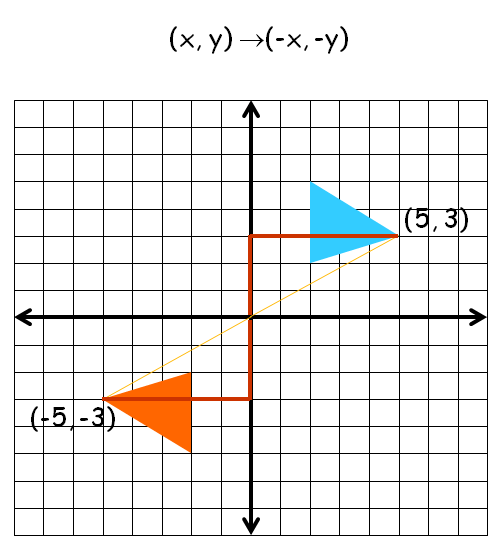
180° Rotation (clock wise and counter clock wise)

Once students understand the rules which they have to apply for rotation transformation, they can easily make rotation transformation of a figure.

For example, if we are going to make rotation transformation of the point (5, 3) about 90° (clock wise rotation), after transformation, the point would be (3, -5).

Here the rule we have applied is (x, y) ------> (y, -x). 

So we get ( 5, 3 ) -------> ( 3, -5 ).

Let us consider the following example to have better understanding of reflection.

Question :

Let A ( -2, 1), B (2, 4) and C (4, 2) be the three vertices of a triangle. If this triangle is rotated about 90° clockwise, what will be the new vertices A' , B' and C' ?

Solution :

Step 1 :

First we have to know the correct rule that we have to apply in this problem.

Step 2 :

Here triangle is rotated about 90° clock wise. So the rule that we have to apply here is (x , y) -------> (y , -x)

Step 3 :

Based on the rule given in step 1, we have to find the vertices of the reflected triangle A'B'C'

Step 4 :

(x, y) -----> (y, -x)

A(-2, 1) -------> A'(1, 2)

B(2, 4) -------> B'(4, -2)

C(4, 2) -------> C'(2, -4)

Step 5 :

Vertices of the reflected triangle are

A'(1, 2), B(4, -2) and C'(2, -4)  

How to sketch the rotated figure ?

1. First we have to plot the vertices of the pre-image.

2. In the above problem, the vertices of the pre-image are

A(-2, 1), B(2, 4) and C(4, 2)

3. When we plot these points on a graph paper, we will get the figure of the pre-image (original figure).

4. When we rotate the given figure about 90° clock wise, we have to apply the formula

(x, y) -------> (y, -x) 

5. When we apply the formula, we will get the following vertices of the image (rotated figure).

6. In the above problem, vertices of the image are

A'(1, 2), B'(4, -2)  and C'(2, -4)

7. When plot these points on the graph paper, we will get the figure of the image (rotated figure).

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and Venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6