ROTATIONS

A rotation is a transformation in which a figure is turned about a fixed point. The fixed point is the center of rotation. Rays drawn from the center of rotation to a point and its image form an angle called the angle of rotation.

A rotation about a point A through x degrees (x°) is a transformation that maps every point B in the plane to a point B', so that the following properties are true.

1. If B is not point A, then

BA = B'A and ∠BAB' = x°

2. If B is point A, then

B = B'

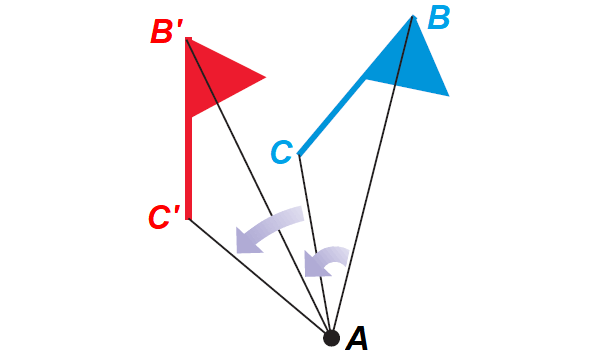
Rotation can be clockwise or counterclockwise as shown below.

Clockwise Rotation of 90° :

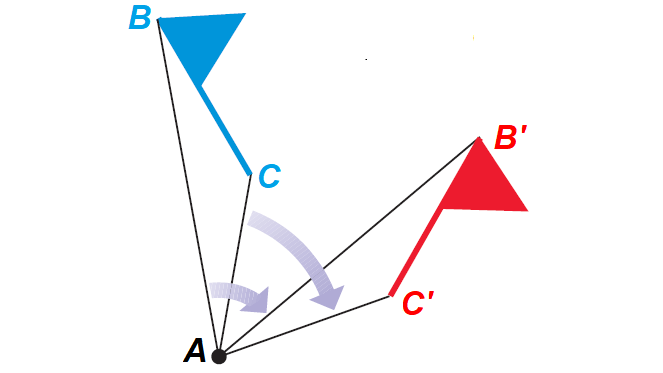
Counterclockwise Rotation of 90° :

Rotation Theorem

A rotation is an isometry.

To prove the Rotation Theorem, we have to show that a rotation preserves the length of a segment. Consider a segment BC that is rotated about a point A to produce B'C'. The three cases to consider are shown below.

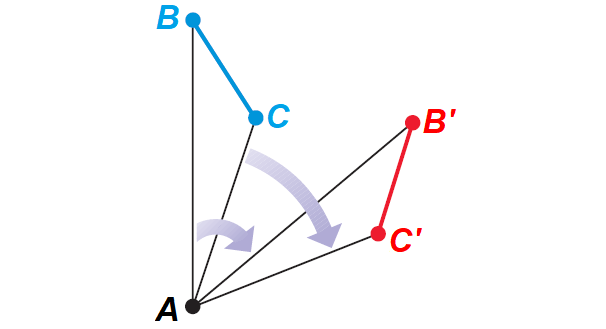
Case 1 :

C, B and A are noncollinear.

It has been illustrated in the diagram shown below.

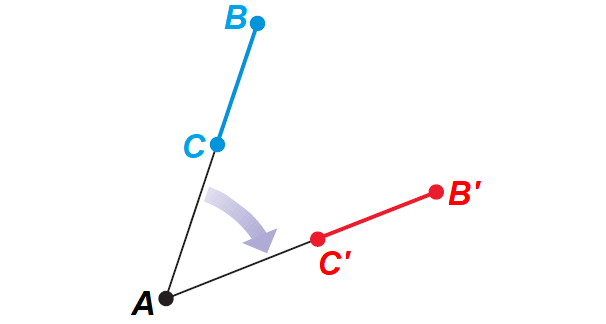
Case 2 :

C, B and A are collinear.

It has been illustrated in the diagram shown below.

Case 3 :

A and C are the same point.

It has been illustrated in the diagram shown below.

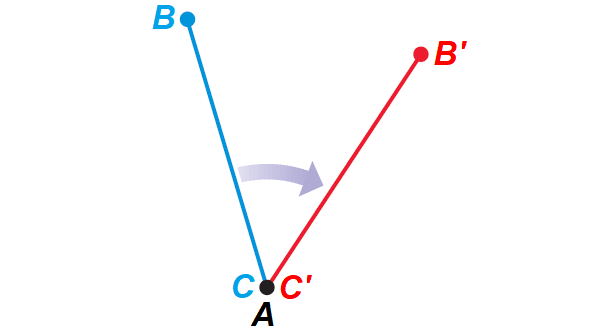
Proof of Case 1 of Rotation Theorem 

Given : A rotation about A maps B onto B' and R onto R'.

Prove : BC ≅ B'C'

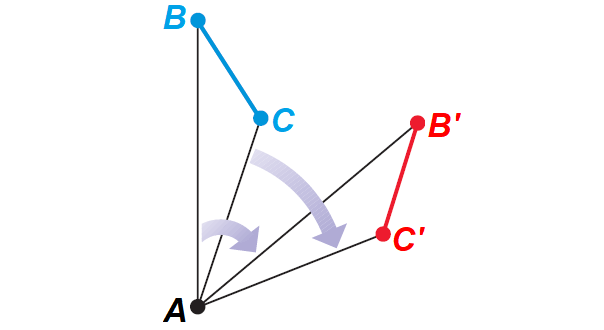
Proof :

By the definition of a rotation,

PQ = PQ' and PR = PR'

Also, by the definition of a rotation,

m∠BAB' = m∠CAC'

We can use the Angle Addition Postulate and the subtraction property of equality to conclude that

m∠BAC = m∠B'AC'

This allows us to use the SAS Congruence Postulate to conclude that

ΔBAC ≅ ΔB'AC'

Because corresponding parts of congruent triangles are congruent,

BC ≅ B'C'

using SAS Congruence Postulate.

Activity : Rotating a Figure

Use the following steps to draw the image of ΔABC after a 120° counterclockwise rotation about point P.

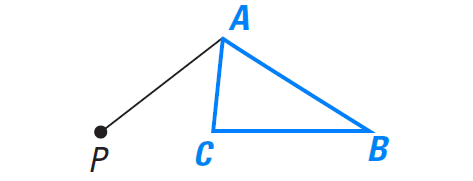
Step 1 :

Draw a segment connecting vertex A and the center of rotation point P.

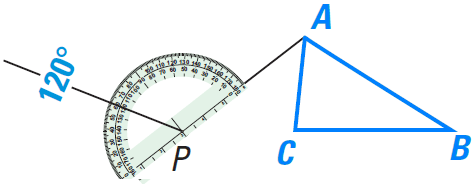
Step 2 :

Use a protractor to measure a 120° angle counterclockwise and draw a ray.

Step 3 :

Place the point of the compass at P and draw an arc from A to locate A'.

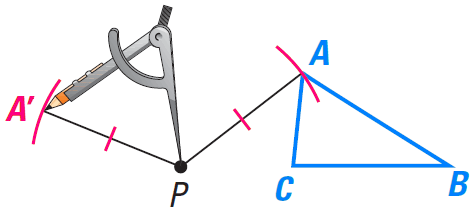
Step 4 :

Repeat steps 1-3 for each vertex. Connect the vertices to form the image.

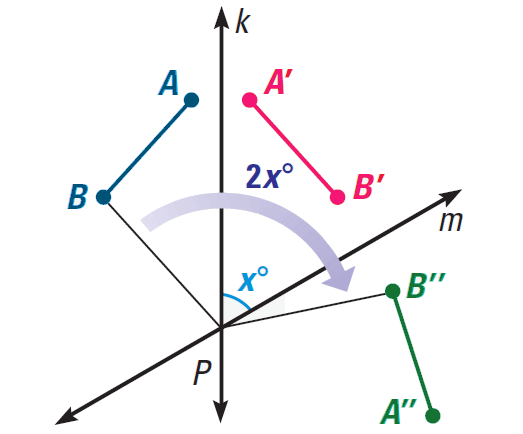
Rotation in Intersecting Lines - Theorem

If lines k and m intersecting at point P, then a reflection in k followed by a reflection in m is a rotation about point P.

In the diagram shown below, the angle of rotation is 2x°, where x° is the measure of the acute or right angle formed by k and m, then

∠BPB" = 2x°

Example :

In the diagram shown below, ΔRST is reflected in line k to produce ΔR'S'T'. This triangle is then reflected in line m to produce ΔR"S"T". Describe the transformation that maps ΔRST to R"S"T".

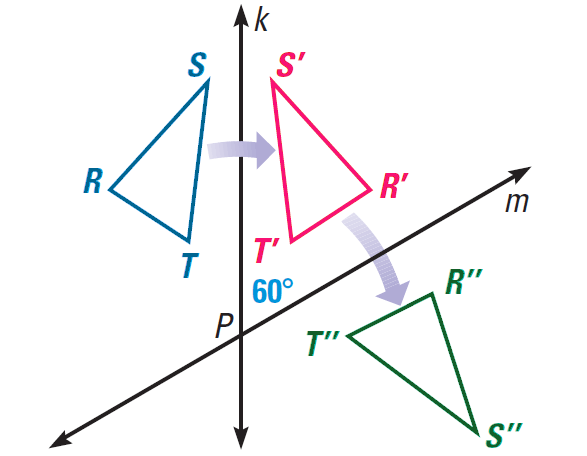
Solution :

The acute angle between lines k and m has a measure of 60°. Applying the above Theorem, we can conclude that the transformation that maps ΔRST to ΔR"S"T" is a clockwise rotation of 120° about point P.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.