SAMPLE QUESTIONS ON SEQUENCE AND SERIES WITH SOLUTIONS

Question 1 :

Prove that n² -n divisible by 2 for every positive integer n.

Solution :

n² -n   =  n(n - 1)

If n is odd, then n - 1 is even.

If n - 1 is odd, then n will be even.

The product of odd number and even number will be an even number.

Hence n² -n is divisible by 2.

Question 2 :

A milk man has 175 litres of cow’s milk and 105 litres of buffalow’s milk. He wishes to sell the milk by filling the two types of milk in cans of equal capacity. Calculate the following

(i) Capacity of a can

(ii) Number of cans of cow’s milk

(iii) Number of cans of buffalow’s milk

Solution :

Since the capacity of two can will be equal, we have to find H.C.F.

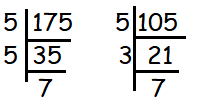
175  =  5² x 7

105  =  5 x 3 x 7

H.C.F  =  5 x 7   =  35

Hence the capacity of each can is 35 liters.

(ii) Number of cans of Cow's milk

To find number of can of cows milk, we have to divide 175 by 35.

175/35  =  5

Hence 5 cans of cow's milk is available.

(iii) Number of cans of buffalow’s milk

To find number of can of cows milk, we have to divide 105 by 35.

105/35  =  3

Hence 3 cans of buffalow’s milk is available.

Question 3 :

When the positive integers a, b and c are divided by 13 the respective remainders are 9, 7 and 10. Find the remainder when a +2b + 3c is divided by 13.

Solution :

Division algorithm :

Divided  =  Divisor x quotient + Remainder

a  =  13q₁ + 9 -------(1)

b  =  13q₂ + 7

2b  =  26q₂ + 14  -------(2)

c  =  13q₃ + 10

3c  =  39q₃ + 30 -------(3)

(1) + (2) + (3)

a + 2b + 3c  =  13q₁ + 9 + 26q₂ + 14 + 39q₃ + 30

  =  13(q₁ + q₂ + q₃) + 53

The remainder is 53.

Question 4 :

Show that 107 is of the form 4q + 3 for any integer q.

Solution :

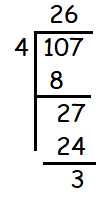
107  =  4(26) + 3

Hence the value pf q is 26.

Question 5 :

If (m +1)^th term of an A.P. is twice the (n +1)^th term, then prove that (3m+1)^th term is twice the (m +n +1)^th term.

Solution :

Let a is the first term of AP and d is the common difference of AP now ,

according to question ,

(m+1)^th term =2 (n+1)^th term 

n^th term of the A.P

t_n  =  a + (n -1) d

a + (m + 1 - 1) d  =  2 {a + (n + 1 - 1) d }

a + md  =  2a + 2nd

(m - 2n) d  =  a ------------(1)

now,

LHS 

(3m + 1)^th term :

  =  a + (3m + 1 - 1) d

  = (m - 2n) d + 3md 

  = 2 (2m - n) d 

RHS

2 (m+n+1)^th term :

  =  2 {a+(m+n+1-1) d}

  =  2 {a+(m+n) d}

  =  2 {(m-2n)d +(m+n) d}

  =  2 (2m-n) d 

Hence proved.

Question 6 :

Find the 12^th term from the last term of the A. P -2,-4,-6,...........-100 .

Solution :

n^th term of the A.P

t_n  =  a + (n -1) d

a = -2, d = -4 - (-2) ==>  d  =  -4 + 2  =  -2 and n = 12

t₁₂  =  -2 + (12 -1) (-2)

t₁₂  =  -2 + (11) (-2)

  =  -2 - 22

t₁₂  =  -24

Hence the 12th term of the A.P is -24.

Question 7 :

Two A.P.’s have the same common difference. The first term of one A.P. is 2 and that of the other is 7. Show that the difference between their 10th terms is the same as the difference between their 21st terms, which is the same as the difference between any two corresponding terms.

Solution :

Let the same common difference of two AP’s is d,

Given that, the first term of first AP and second AP are 2 and 7 respectively, then the AP’s are 

2, (2 + d), (2 + 2d), (2 + 3d),..............

and  7, (7+ d), (7 +2d), (7+3d),…........

Now, 10th terms of first and second AP’s are 2 + 9d and 7 + 9 d, respectively.

So, their difference is 7 + 9d – (2 + 9d) = 5

Also, 21st terms of first and second AP’s are 2 + 20d and 7 + 20d, respectively.

So, their difference is

7 + 20d – (2 + 9d) = 5

Also, if the a„ and bn are the nth terms of first and second AP.

Then, b_n -a_n = [7 + (n-1)d)] – [2 + (n-1)d] = 5

Hence, the difference between any two corresponding terms of such AP’s is the same as the difference between their first terms.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.