SAT MATH QUESTIONS ON ABSOLUTE VALUE

Question 1 :

If |1 - x| > 4 and x is positive, what is one possible value of x?

Answer :

|1 - x| > 4

1 - x > 4  or  1 - x < -4

Since x is positive, one possible value of x satisfying x > 5 is 6. That is

x = 6

Question 2 :

0 < |5/x| < 1

Which of the following values of x satisfies the inequality above?

A) 2

B) 3

C) -3

D) -8

Answer :

0 < |5/x| < 1

A) 2 :

Substitute x = 2 in |5/x|.

|5/2| = 5/2 > 1

When x = 2, the value of |5/x| is not between 0 and 1.

2 does not work.

B) 3 :

Substitute x = 3 in |5/x|.

|5/3| = 5/3 > 1

When x = 3, the value of |5/x| is not between 0 and 1.

3 does not work.

C) -3 :

Substitute x = -3 in |5/x|.

|5/(-3)| = |-5/3|

= 5/3 > 1

When x = -3, the value of |5/x| is not between 0 and 1.

-3 does not work.

D) -8 :

Substitute x = 8 in |5/x|.

|5/8| = |5/8|

= 5/8

The value 5/8 is between 0 and 1, that is

0 < 5/8 < 1

When x = -8, the value of |5/x| is between 0 and 1.

-8 works.

The correct answer choice is (D).

Question 3 :

A bakery standardizes muffins to weigh between 1¾ and 2¼ounces. If m is the weight of muffin from this bakery, which of the following inequalities expresses the following possible values of m?

A) |m - 1¾| < ¼

B) | m - 2| < ¼

C) |m - 2| < ½

D) |m - 1¾| < ½

Answer :

It's kind of solving absolute value inequality in reverse order. Here, the boundary values of m are given and we have to find the absolute value inequality which gives the given boundary values ¾ and 2¼.

Find the middle value of the two boundary values.

Middle value of 1¾ and 2¼ is their average :

= (1¾ + 2¼) ÷ 2

= 4 ÷ 2

= 2

Since 1¾ and 2¼ are the boundary values of m,

1¾ < m < 2¼

Subtract the middle value.

(1¾ - 2) < (m - 2) < (2¼ - 2)

-¼ < (m - 2) < ¼

We know that

-A < x < A ----> |x| < A

So, we have

-¼ < (m - 2) < ¼ ----> |m - 2| < ¼

The correct answer choice is (B).

Question 4 :

If |x + 3| < 2, which of the following could be the value of |x|?

A) 1

B) 4

C) 6

D) 10

Answer :

|x + 3| < 2

x + 3 < 2  or  x + 3 > -2

x < -1  or  x > -5

Combined inequality of x < -1 and x > -5 :

-5 < x < -1

The possible integer values of x are -4, -3, -2.

Substitute x = -4, -3, -2, -1 in |x|.

|-4| = 4

|-3| = 3

|-2| = 2

The correct answer choice is (B).

Question 5 :

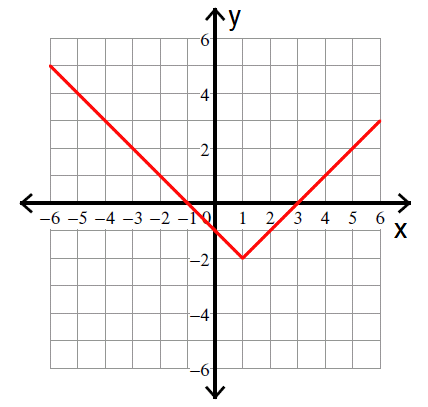
Which of the following could be the equation of the function graphed in the xy-plane above?

A) y = -|x - 1| - 2

B) y = |x - 1| - 2

C) y = |x - 1| + 2

D) y = |x + 1| - 2

Answer :

The graph of y = |x| is a V-shape centered at the origin.

The graph above is also V-shaped. But, it is shifted 1 unit to the right and 2 units down.

After shifting 1 unit to the right, y = |x| becomes

y = |x - 1|

Further shifting of 2 units down,

y = |x - 1| - 2

The correct answer choice is (B).

Question 6 :

If |x - 10| = y, x < 10, then which of the following is equivalent to (y - x)?

A) -10

B) 10

C) 2y - 10

D) 10 - 2y

Answer :

Assume some value for x such that x < 10, say x = 3.

In |x - 10| = y, substitute x = 3 and find the value of y.

y = |3 - 10|

y = |-7|

y = 7

Find the value of (y - x).

y - x = 7 - 3

y - x = 4

Among the given answer choices, pick the one which gives the result 4 when y = 7.

The correct answer choice is (C).

Note :

Instead of assuming x = 3, you can assume any value for x such that x < 10 and solve this problem. You will get the same answer.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.