SAT MATH : Solving Problem Using The Triangle Midsegment Theorem

Problem :

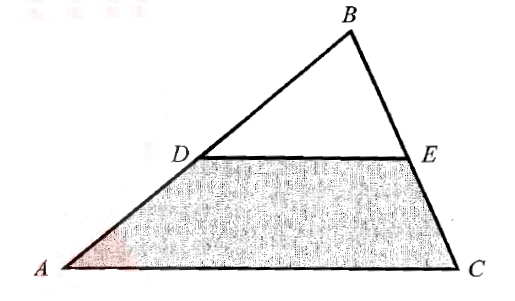
In the figure above, D and E are the midpoints of AB and BC respectively. If the area of the shaded region is 42, what is the area of triangle ABC?

Solution :

Given : DE is the line segment joining the midpoints of the sides of the triangle AB and BC respetively.

By The Triangle Midsegment Theorem, the line segment DE is parallel to the third side AC and the length of DE is half of the length of AC.

If AC = 2b, then DE = b. Draw two perpendiculars BF and FG as shown in the figure below.

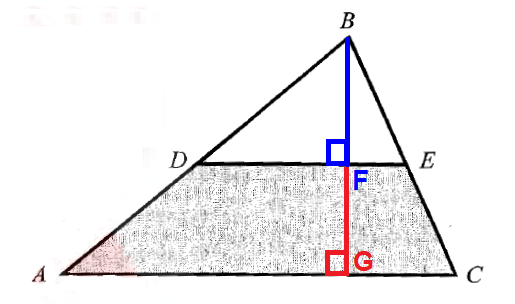
Let BF = h. Then FG = h. Because the line segment DE is joining the midpoints of the sides of the triangle AB and BC.

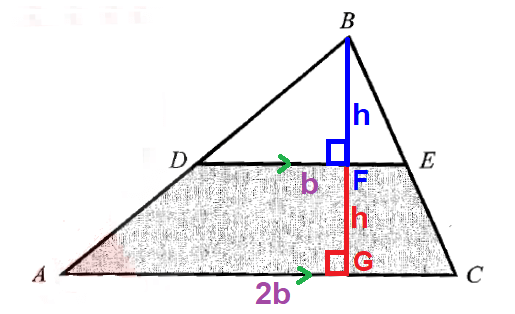
In the figure above, ADEC is a trapezoid (shaded region). Because it has two parallel sides DE and AC.

Area of the trapezoid ADEC (shaded region) :

Given : Area of the shaded region is 42.

Then, we have

Multiply both sides by ³⁄₂.

bh = 28

In the given figure, area of the triangle DBE : 

Substitute bh = 28.

= 14

Area of the triangle ABC ;

= Area of the shaded region +  Area of the triangle DBE

= 42 + 14

= 56 square units

Video Lesson

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.