SAT MATH - SOLVING WORD PROBLEMS

Questions 1 - 3 refer to the following information.

The manager of an apartment building needs an electrician to repair the power generator for the building. The table below shows the fixed amount for a time service call and hourly charges for two different companies.

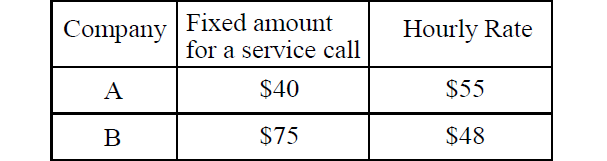
Problem 1 :

Which of the following equations gives the total cost y, of repairing the power generator in terms of the total number of hours x, from company A?

(A)  y = 48x + 75

(B)  y = 75x + 48

(C)  y = 40x + 55

(D)  y = 55x + 40

Solution :

If the apartment manager hires an electrician from company A, he needs to pay 55 dollars per hour. So for x hours, he has to pay 55x dollars plus 40 dollars for a service call. The total cost y of repairing the power generator will be

y = 55x + 140

Therefore, the correct answer is option (D).

Problem 2 :

For what number of hours x, will the total cost of repairing the generator for company B be less than or equal to the total cost of repairing the generator for company A?

(A)  x ≥ ⁵⁄₂

(B)  x ≤ ⁵⁄₂

(C)  x ≥ 5

(D)  x ≤ 5

Solution :

The total cost y of repairing for company B :

y = 48x + 75

The total cost y of repairing for company A :

y = 55x + 40

Given : The total cost of repairing for company B be less than or equal to the total cost of repairing A.

48x + 75 ≤ 55x + 40

75 ≤ 7x + 40

35 ≤ 7x

5 ≤ x

x ≥ 5

Therefore, the correct answer is option (C).

Problem 3 :

Company B’s total cost y, is the fixed amount for a service call plus the hourly rates. If the relationship between Company B’s total cost y, and the number of hours x, is graphed in the xy-plane, what does the slope of the line represent?

(A)  Fixed amount for a service call

(B)  Hourly Rate

(C)  Total amount for one day

(D)  Total amount for repairing the power generator

Solution :

y ---> total cost

x ----> number of hours

slope = cost per hour

If the relationship is graphed on the xy-plane, the slope represents the hourly rate.

Therefore, the correct answer is option (B).

Problem 4 :

Apex Car Rental company charges a flat fee of $40.00 per day plus $0.75 per mile to rent a car. Jason Car Rental company charges a flat fee of $64.00 per day plus $0.60 per mile to rent a car. If a car is rented for three days, at how many miles would the rental charges of the two companies be the same?

(A)  480

(B)  450

(C)  420

(D)  380

Solution :

When a car is rented for three days and driven for x miles, the rental charges of Apex Car Rental :

= 0.75x + 3 ⋅ 40

= 0.75x + 120

the rental charges of Jason Car Rental :

= 0.6x + 3 ⋅ 64

= 0.6x + 192

If the rental charges of the two companies be the same,

0.75x + 120 = 0.6x + 192

0.15x = 72

x = 480

The rental charges of the two companies woud be the same for 480 miles.

Therefore, the correct answer is option (A).

Problem 5 :

It took Sara a total of 42 minutes to jog from home to the park and back again, by the same path. If she averaged 8 miles per hour going to the park and 6 miles per hour coming back, what is the distance from her home to the park?

(A)  2.4 miles

(B)  2.8 miles

(C)  3.2 miles

(D)  3.6 miles

Solution :

Let d be the distance in miles from Sara’s home to the park.

Formula to find the time :

Time taken when Tara goes to the park at the rate of 8 miles per hour :

= ᵈ⁄₈ hours

Time taken when Tara comes back home at the rate of 6 miles per hour :

= ᵈ⁄₆ hours

Given : Total time is 42 minues.

42 minutes = ⁴²⁄₆₀ hours

42 minutes = ⁷⁄₁₀ hours

The least common multiple of (8, 6. 10) = 120.

Multiply both sides of the above equation by 120 to get rid of the denominators 8, 6 and 10.

d = 2.4

The distance from her home to the park is 2.4 miles.

Therefore, the correct answer is option (A).

Problem 6 :

Carl drove from his home to the beach at an average speed of 50 mph and returned home along the same route at an average speed of 30 mph. His total driving time for the trip was 2 hours. Solving which of the following systems of equations yields x, the time it took for Carl to drive to the beach and y, the time spent for the return trip?

(A)  x = y + 2  and  50x = 30y

(B)  x + y = 2  and  30x = 50y

(C)  x + y = 2  and  50x = 30y

(D)  y = x + 2  and  30x = 50y

Solution :

x ---> time taken to drive to the beach

y ---> time taken for the return trip

Given : The trip was 2 hours.

x + y = 2

We know that

distance = speed ⋅ time

Home to the beach, speed is 50 mph and time is x hours.

Distance from home to the beach :

= 50 ⋅ x

= 50x

Beach to the home, speed is 30 mph and time is y hours.

Distance from beach to the home :

= 30 ⋅ y

= 30y

50x = 30y

The sytem of equations :

x + y = 2

50x = 30y

Therefore, the correct answer is option (C).

Problem 7 :

To join Ace Gym, one must pay a $180 membership fee plus dues of $35 per month. To join Best Gym, one must pay a $300 membership fee plus dues of $23 per month. At how many months would the total cost of either gym be the same?

(A)  7

(B)  8

(C)  9

(D)  10

Solution :

Let y be the total cost and x be the number of months.

Ace Gym ----> y = 35x + 180

Best Gym ----> y = 23x + 300

If the total cost of either gym be the same,

y = y

35x + 180 = 23x + 300

12x = 120

x = 10

The total cost of either gym would be the same for 10 months.

Therefore, the correct answer is option (D).

Problem 8 :

At a county fair the admission is $8.00 and each ride costs $1.25. If you go to the fair with $20.00, what is the maximum number of rides you can go on?

(A)  8

(B)  9

(C)  10

(D)  11

Solution :

Let r be the number of rides. Then the total cost is

= 1.25r + 8

The total cost should not exceed $20.

1.25r + 8 ≤ 20

1.25r ≤ 12

r ≤ 9.6

The maximum intger value that r can have is 9. That is, the maximum number of rides is 9.

Therefore, the correct answer is option (B).

Problem 9 :

A car averages 18 miles per gallon of gas for city driving and 27 miles per gallon of gas for highway driving. What is the total number of gallons of gas needed to drive 6x miles in the city and 18x miles on the highway?

(A)  x

(B)  2x

(C)  3.5x

(D)  4.5x

Solution :

City Driving :

18 miles ----> 1 gallon

1 mile ----> ¹⁄₁₈ gallons

(6x)(1 mile) ----> (6x)(¹⁄₁₈ gallons)

6x miles ----> ˣ⁄₃ gallons

Highway Driving :

27 miles ----> 1 gallon

1 mile ----> ¹⁄₂₇ gallons

(18x)(1 mile) ----> (18x)(¹⁄₂₇ gallons)

18x miles ----> ²ˣ⁄₃ gallons

Total number of gallons of gas needed to drive 6x miles in the city and 18x miles on the highway :

= ˣ⁄₃ gallons + ²ˣ⁄₃ gallons

= (ˣ⁄₃ + ²ˣ⁄₃) gallons

= ⁽ˣ ⁺ ²ˣ⁾⁄₃ gallons

= ³ˣ⁄₃ gallons

= x gallons

Therefore, the correct answer is option (A).

Problem 10 :

One section of a grocery store display only water bottles. The water bottles are in either 6-bottle packages or 8-bottle packages. Let x represent the number of 6-bottle packages and y represent the number of 8-bottle packages. The total number of packages displayed are 270 and the total number of bottles are 1860. To find the values of variables x and y, which of the following systems of equations can be used?

(A)  x + y = 1860  and  6x + 8y = 270

(B)  6x + 8y = 1860  and  x + y = 270

(C)  8x + 6y = 1860  and  x + y = 270

(D)  x + y = 1860  and  8x + 6y = 270

Solution :

x ----> number of 6-bottle packages

y ----> number of 8-bottle packages

Given : The total number of packages displayed are 270.

x + y = 270

Given : The total number of bottles are 1860.

6x + 8y = 1860

The system of equations :

x + y = 270

6x + 8y = 1860

Therefore, the correct answer is option (B).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.