SCATTER PLOTS AND TREND LINES

Graphing a Scatter Plot from Given Data

Example 1 : 

The table shows the number of species added to the list of endangered and threatened species in the United States during the given years. Graph a scatter plot using the given data.

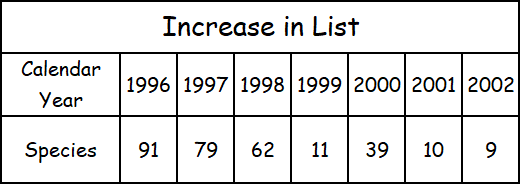
Source: U.S. Fish and Wildlife Service.

Solution : 

Use the table to make ordered pairs like (1996, 91) for the scatter plot.

The x-value represents the calendar year and the y-value represents the number of species added.

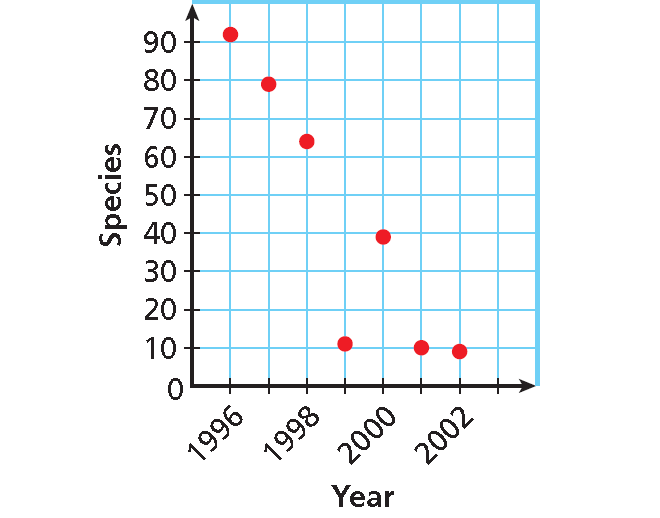
Plot the ordered pairs.

Correlations

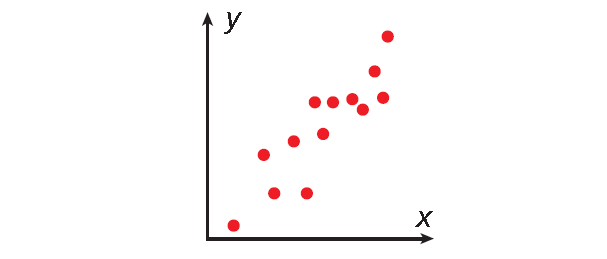
Positive Correlation

Both sets of data values increase.

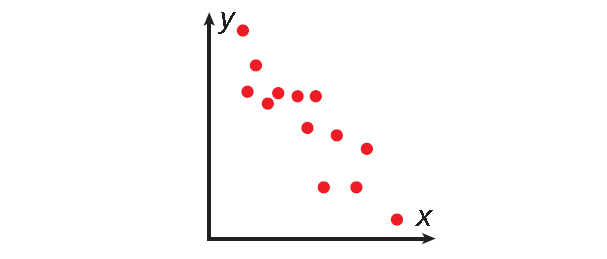
Negative Correlation

One set of data values increases as the other set decreases.

No Correlation

There is no relationship between the data sets.

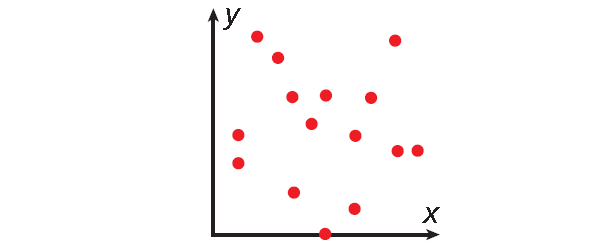
In the endangered species graph in example 1 above, as time increases, the number of new species added decreases. So the correlation between the data is negative.

Describing Correlations from Scatter Plots

Example 2 : 

Describe the correlation between TV watching and test score illustrated by the scatter plot.

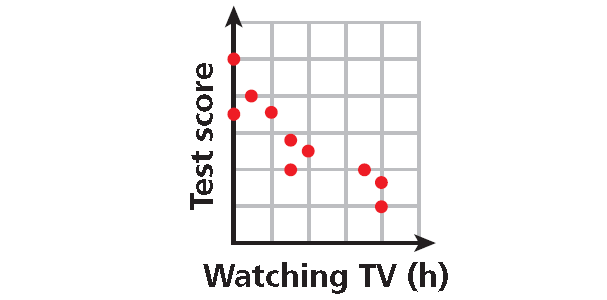
Solution : 

As the number of hours spent watching TV increased, test scores decreased.

There is a negative correlation between the two data sets.

Identifying Correlations

Identify the correlation you would expect to see between each pair of data sets. Explain.

Example 3 : 

The number of empty seats in a classroom and the number of students seated in the class. 

Solution : 

You would expect to see a negative correlation. As the number of students increases, the number of empty seats decreases.

Example 4 : 

The number of pets a person owns and the number of books that person read last year.

Solution : 

You would expect to see no correlation. The number of pets a person owns has nothing to do with how many books the person has read.

Example 5 : 

The monthly rainfall and the depth of water in a reservoir. 

Solution : 

You would expect to see a positive correlation. As more rain falls, there is more water in the reservoir.

Matching Scatter Plots to Situations

Example 6 : 

Choose the scatter plot that best represents the relationship between the number of days since a sunflower seed was planted and the height of the plant. Explain. The x-value represents time (days) and the y-value represents the height (in.). 

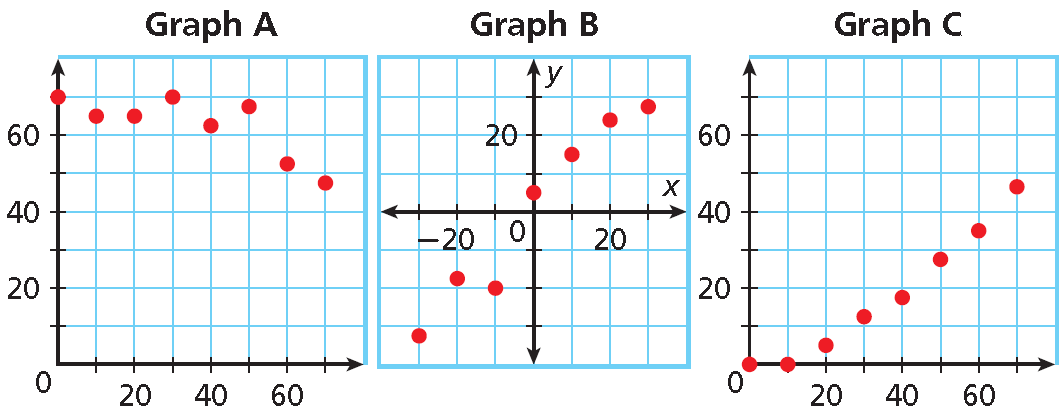
Solution :

Graph A : 

There will be a positive correlation between the number of days and the height because the plant will grow each day.

Graph A has a negative correlation, so it is incorrect.

Graph B : 

Neither the number of days nor the plant heights can be negative.

Graph B shows negative values, so it is incorrect.

Graph C : 

This graph shows all positive coordinates and a positive correlation, so it could represent the data sets.

Graph C is the correct scatter plot.

Fund-Raising Application

Example 7 : 

The scatter plot shows a relationship between the total amount of money collected and the total number of rolls of wrapping paper sold as a school fund-raiser. Based on this relationship, predict how much money will be collected when 175 rolls have been sold.

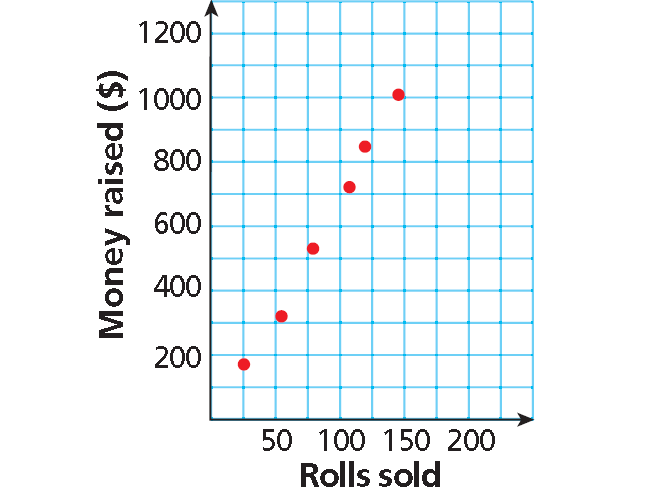
Draw a trend line and use it to make a prediction.

Solution :

Draw a line that has about the same number of points above and below it. Your line may or may not go through data points.

Find the point on the line whose x-value is 175. The corresponding y-value is 1200.

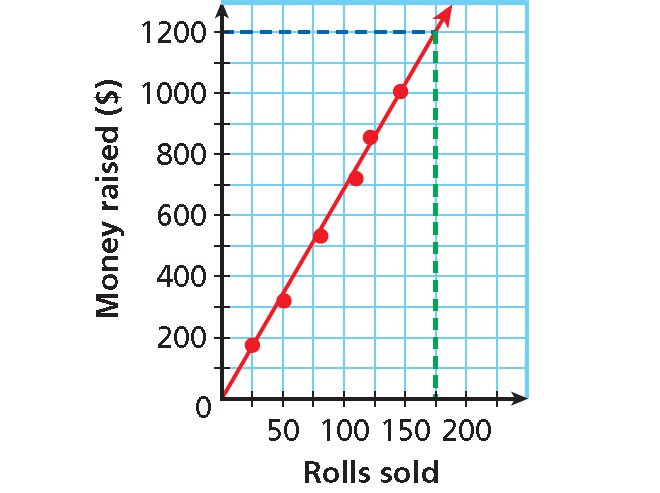
Based on the data, $1200 is a reasonable prediction of how much money will be collected when 175 rolls have been sold.

Example 8 : 

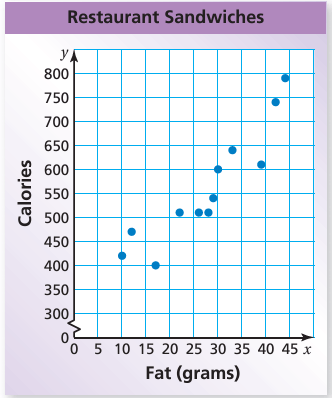
The scatter plot below shows the total fat (in grams) and the total calories in 12 restaurant sandwiches.

a. How many calories are in the sandwich that contains 17 grams of fat?

b. How many grams of fat are in the sandwich that contains 600 calories?

c.  What tends to happen to the number of calories as the number of grams of fat increases? 

Solution :

a)  Draw a horizontal line from the point that has an x-value of 17. It crosses the y-axis at 400. So, the sandwich has 400 calories.

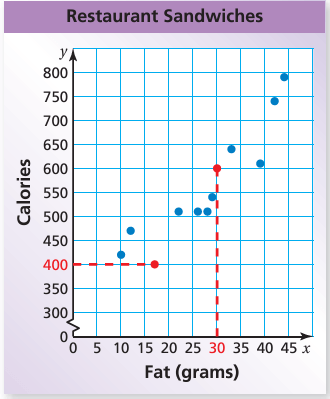
b)  Draw a vertical line from the point that has a y-value of 600. It crosses the x-axis at 30.

So, the sandwich has 30 grams of fat

c)  Looking at the graph, the plotted points go up from left to right. So, as the number of grams of fat increases, the number of calories increases

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.