SCIENTIFIC NOTATION RULES

Scientific notation is a standard way of writing very large and very small numbers so that they’re easier to both compare and use in computations. 

Every number in the scientific notation must be in the form of 

a x 10ⁿ

where 1 ≤ a < 10 and n must be a positive or negative integer. 

To convert a number into scientific notation, first we have to identify where the decimal point and non zero digit come. 

There are two cases in it. 

Case 1 : 

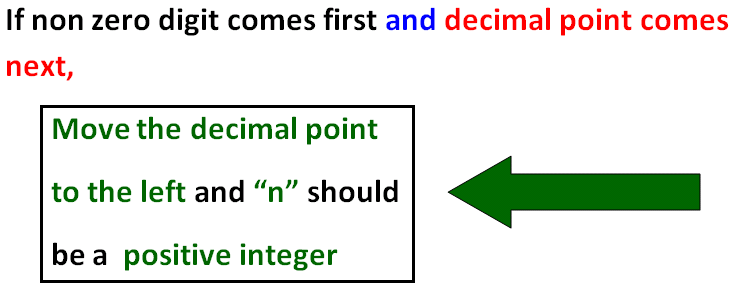
To move the decimal point to the left, we have to count number of digits as explained in the example given below. 

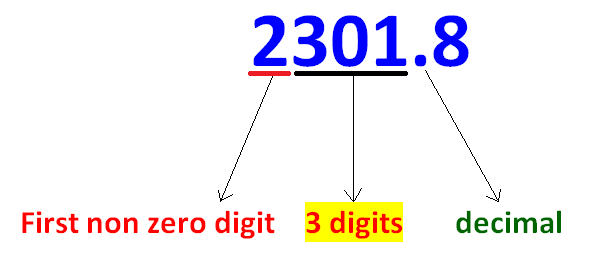
According to the example given above, we have to move the decimal point 3 digits to the left and exponent of 10 should be 3 (positive integer)

When we do so, we get the scientific notation of the given number. 

So,

2301.8 = 2.3018 x 10³

Case 2 : 

To move the decimal point to the right, we have to count number of digits as explained in the example given below. 

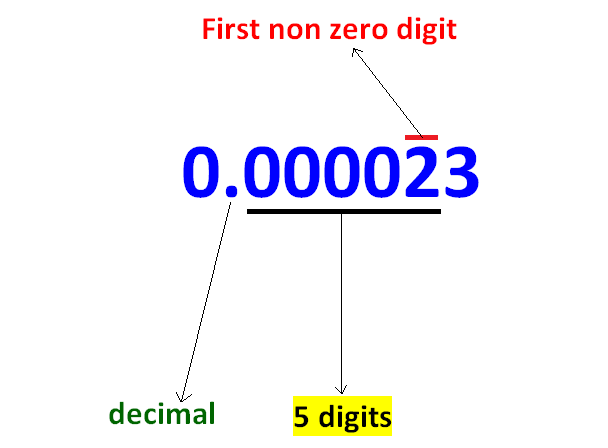
According to the example given above, we have to move the decimal point 5 digits to the right and exponent of 10 should be -5 (negative integer)

When we do so, we get the scientific notation of the given number. 

So,

0.000023 = 2.3 x 10^-5

Important Note: 

If we don't find decimal point at anywhere of the given number, we have to assume that there is decimal point at the end of the number.

For example, 

2300000 ----> 2300000.

Here, the non zero digit comes first and decimal point comes next. So we have to apply case 1 to convert this number into scientific notation.  

Solved Problems

Write the following numbers in scientific notation.

Problem 1 :

0.0007

Solution :

Here decimal point comes first at non zero digit comes next. 

We have to move the decimal point to the right. 

Number of digits from the decimal point to the first non zero digit is 4.

So, the decimal point has to be moved 4 digits to the right and exponent of 10 should be -4 (negative integer)

Therefore, the scientific notation of 0.0007 is

7 x 10^-4

Problem 2 :

Write the given number in scientific notation. 

28000

Solution :

Here we don't find decimal point in 28000. So we have to assume that there is decimal point at the end . 

Then, 28000 ----> 28000.

Here non zero digit comes first and decimal point comes next. 

We have to move the decimal point to the left. 

Number of digits between the 1^st non-zero digit and the decimal point is 4.

So, the decimal point has to be moved 4 digits to the left and exponent of 10 should be 4 (positive integer)

= 28000

= 2.8000 x 10⁴

= 2.8 x 10⁴

Problem 3 :

64 x 10³

Solution :

Here we don't find decimal point in 64x 10³. So we have to assume that there is decimal point at the end of 64 

Then, 

64 x 10³ ----> 64. x 10³

Here non zero digit comes first and decimal point comes next. 

We have to move the decimal point to the left. 

Number of digits between the 1^st non zero digit and the decimal point is 1.

So, the decimal point has to be moved 1 digit to the left and exponent of 10 should be 2 (positive integer)

= 64. x 10³

= 6.4 x 10¹ x 10³

= 6.4 x 10^{1 + 3}

= 6.4 x 10⁴

Problem 4 :

44 x 10^-2

Solution :

Here we don't find decimal point in 44 x 10^-2 So we have to assume that there is decimal point at the end of 44 

Then, 

44 x 10^-2 ----> 44. x 10^-2 

Here non-zero digit comes first and decimal point comes next. 

We have to move the decimal point to the left. 

Number of digits between the 1^st non zero digit and the decimal point is 1.

So, the decimal point has to be moved 1 digit to the left and exponent of 10 should be 1 (positive integer)

= 44. x 10^-2

= 4.4 x 10¹ x 10^-2

= 4.4 x 10^{1 - 2}

= 4.4 x 10^-1

Problem 5 :

0.075 x 10^-3

Solution : 

Here decimal point comes first and non-zero digit comes next. 

We have to move the decimal point to the right. 

Number of digits from the decimal point to the first non zero digit is 2.

So, the decimal point has to be moved 2 digits to the right and exponent of 10 should be -2 (negative integer)

= 0.075 x 10^-3

= 7.5 x 10^-2 x 10^-3

= 7.5 x 10^-2-3

= 7.5 x 10^-5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.