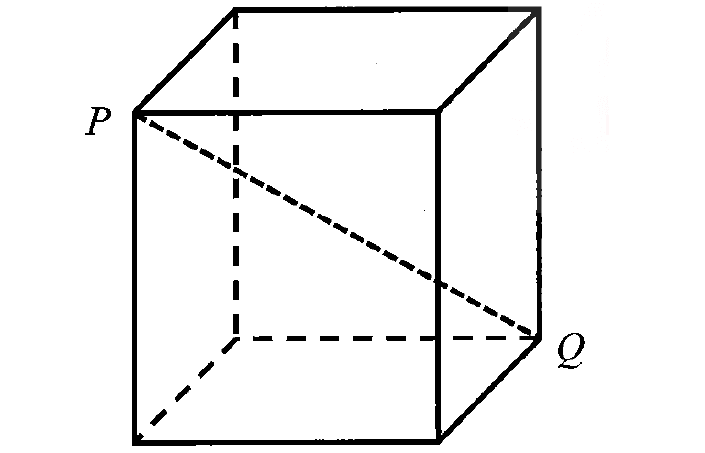
SECTION FORMULA INTERNALLY AND EXTERNALLY

We use the section formula to find the point which divides the line segment in a given ratio.

The point P which divides the line segment joining the two points A (x₁,  y₁) and B (x₂, y₂) internally in the ratio l : m is  

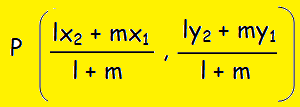
If P divides a line segment AB joining the two points 

A (x₁,  y₁) and B (x₂, y₂) externally in the ratio l : m is,

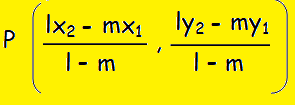
Example 1 :

Find the coordinates of the point which divides the line segment joining (-3, 5) and (4, -9) in the ratio 1:6 internally.

Solution :

Let  A (-3, 5) and B (4, -9)

Section formula internally 

=  (lx₂+mx₁)/(l+m),  (ly₂+my₁)/(l+m)

l = 1 and m = 6    

=  [(1(4)+(6(-3)]/(1+6) , [(1(-9)) + 6(5)]/(1+6)

=  (4-18)/7, (-9 + 30)/7

=  -14/7, 21/7

=  (-2, 3) 

Example 2 :

Let A (-6 , -5) and B(-6 , 4) be the two points such that a point  P on the line AB satisfies AP = (2/9) AB.

Find the point P.

Solution :

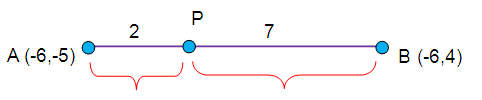
AP  =  (2/9) AB

9AP  =  2(AP+PB)

9AP  =  2AP + 2PB

9AP – 2AP  =  2PB

7AP  =  2PB

AP/AB  =  2/7

AP:PB  =  2:7

So P divides the line segment in the ratio 2:7

Section formula internally

=   (lx₂+mx₁)/(l+m),  (ly₂+my₁)/(l+m)

l = 2, m = 7    

=  [(2(-6)+7(-6)]/(2+7), [(2x(4)+7(-5)]/(2+7)

=  (-12-42)/9, (8-35)/9

=  -54/9, -21/7

=  (-6, -3)

Example 3 :

Find the points of trisection of the line segment joining the points A (2, -2) and B (-7, 4).

Solution :

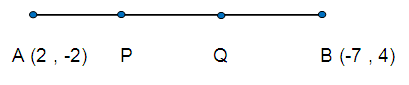
AP = 1, PQ = 1, QB = 1

=   (lx₂+mx₁)/(l+m),  (ly₂+my₁)/(l+m)

P divides the line segment in the ratio 1:2

l = 1, m = 2    

=  [(1(-7)+2(2)]/(1+2),  [1(4)+2(-2)]/(1+2)

=  (-7+4)/3, (4-4)/3

=  -3/3 , 0/3

=  P (-1 , 0)

Q divides the line segment in the ratio 2:1

l = 2, m = 1    

=  [2(-7)+1(2)]/(2+1), [2(4)+1(-2)]/(2+1)

=  (-14+2)/3, (8-2)/3

=  -12/3 , 6/3

=  Q (-4, 2)

Example 4 :

Find the ratio in which x axis divides the line segment joining the points (6, 4) and (1,- 7).

Solution :

Let l : m be the ratio of the line segment joining the points (6, 4) and (1, -7) and let p(x, 0) be the point on the x axis

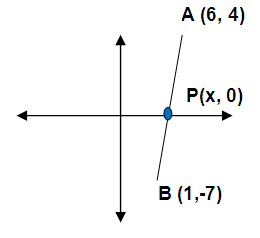
Section formula internally =  

(lx₂+mx₁)/(l+m),  (ly₂+my₁)/(l+m)

(x, 0)  =  [l(1)+m(6)]/(l+m) , [l(-7)+m(4)]/(l+m)

(x , 0)  =  [l+6m]/(l+m) , [-7l+4m]/(l+m)

Equating y-coordinates 

[-7l+4m]/(l+m)  =  0

-7l+4m  =  0

-7l  =  -4m

l/m  =  4/7

l : m = 4 : 7

So, x-axis divides the line segment in the ratio 4:7.

=  Q (-4, 2)

Example 5 :

Find the coordinates of the point which divides the line segment joining the points A(4, -3) and B(9, 7) in the ratio 3 : 2.

Solution :

The given ratio is 3 : 2, l : m = 3 : 2

A(4, -3) and B(9, 7)

= (lx₂ + mx₁)/(l + m),  (ly₂ + my₁)/(l + m)

= [3(9) + 2(4)] / (3 + 2), [3(7) + 2(-3)] / (3 + 2)

= [27 + 8] / 5, [21 - 6] / 5

= 35/5, 15/5

= (7, 3)

So, the required point which is dividing the line segment in the ratio 3 : 2 is (7, 3).

Example 6 :

Find the ratio in which the point P(-3, a) divides the join A(-5, 4) and B(-2, 3). Also find the value of a.

Solution :

The required ratio is l : m, the point which divides the line segment is P(-3, a).

(lx₂ + mx₁)/(l + m),  (ly₂ + my₁)/(l + m)

[l(-2) + m(-5)] / (l + m), [l(3) + m(4)] / (l + m) = (-3, a)

[-2l - 5m] / (l + m), [3l + 4m] / (l + m) = (-3, a)

Equating x and y-coordinates, we get

[-2l - 5m] / (l + m) = -3

-2l - 5m = -3(l + m)

-2l - 5m = -3l - 3m

-2l + 3l = -3m + 5m

l = 2m

l/m = 2/1

l : m = 2 : 1

So, the required ratio is 2 : 1.

[3l + 4m] / (l + m) = a

[3(2) + 4(1)] / (2 + 1) = a

(6 + 4) / 3 = a

a = 10/3

So, the value of a is 10/3.

Example 7 :

If the ratio in which the point P(a, 1) divides the join of A(-4, 4) and B(6, -1). Also find the value of a.

Solution :

The required ratio is l : m, the point which divides the line segment is P(a, 1).

(lx₂ + mx₁)/(l + m),  (ly₂ + my₁)/(l + m)

[l(6) + m(-4)] / (l + m), [l(-1) + m(4)] / (l + m) = (a, 1)

[6l - 4m] / (l + m), [-l + 4m] / (l + m) = (a, 1)

Equating x and y-coordinates, we get

[6l - 4m] / (l + m) = a

 [-l + 4m] / (l + m) = 1

-l + 4m = l + m

-l - l = m - 4m

-2l = -3m

2l = 3m

l/m = 3/2

So, the required ratio is l : m is 3 : 2.

Applying the value of l and m, we get

[6l - 4m] / (l + m) = a

[6(3) - 4(2)] / (3 + 2) = a

a = (18 - 8)/5

a = 10/5

a = 2

So, the required value of a is 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.