SECTOR PRACTICAL PROBLEMS FOR GRADE 11

Example 1 :

The perimeter of a certain sector of a circle is equal to the length of the arc of a semi-circle having the same radius. Express the angle of the sector in degrees, minutes and seconds.

Solution :

Perimeter of sector  =  l + 2r

(let "l" be the length of the arc) 

length of the arc of the semi circle  =  πr 

πr =  2r + L 

L =  πr - 2r 

L  =  r (π - 2) 

L  =  r (3.14 -2) 

L  =  1.14 r 

angle of sector  =  1.14r/r 

  =  1.14 rad 

  =  65.29 degrees 

  =  65^◦27' 16'''(Approximately)

Example 2 :

An airplane propeller rotates 1000 times per minute. Find the number of degrees that a point on the edge of the propeller will rotate in 1 second.

Solution :

As per the question :

An airplane propeller rotates 1000 times per minute.

  =  1000 rotations / 1 minute

  =  1000 rotations / 60 seconds

  =  50 rotations / 3 seconds

  =  (360 rotations / seconds) ⋅ (50 rotations/3 seconds)

  =  (120 ⋅ 50)/3

  =  6000 rotations per second.

Example 3 :

A train is moving on a circular track of 1500 m radius at the rate of 66 km/hr. What angle will it turn in 20 seconds?

Solution :

Given - The radius of the circular curve = 1500 m

Speed of the train = 66 km per hour

Speed of the train converted to m/second

  =  (66 ⋅ 1000)/3600

  =  66000/3600

Speed of the train = 18.333 m per second

In 1 second, distance is covered = 18.333 m

In 20 seconds, distance is covered = 18.333 (20)

  =  366.66 m

Angle turned by the train moving on the circular curve in 20 seconds  = arc it made by moving on circular curve/radius of the circular curve

  =  366.66/1500

  = 0.244 radian

In order to convert this radian measurement to degree, we have to multiply it by 180/π

Hence, the trained turned by  0.2444 Radian (angular measurement) in 20 seconds which is equal to 14 degrees (approximately).

Example 4 :

A circular metallic plate of radius 8 cm and thickness 6 mm is melted and molded into a pie (a sector of the circle with thickness) of radius 16 cm and thickness 4 mm. Find the angle of the sector.

Solution :

Volume of circle with thickness  =  πr² ⋅ thickness

 radius  =  8 cm, thickness  =  6 mm  =  (6/10) cm

Volume of circle with thickness  =  π(8)²⋅ (6/10)

  =  38.4 π cm³

Now, the volume of the remolded pie will be the product of the area of the pie and the thickness of the pie.

Now the area of the pie is

Area of sector  =    (θ/360) ⋅ π r²

Radius of new pie  =  16 cm, thickness  = 4mm  =  (4/10) cm

  =  (θ/360) ⋅ π (16)² ⋅ (4/10)

Now, the volume of the circular metallic plate = the volume of the remolded pie

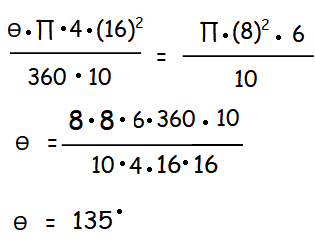
Hence the required angle is 135 degree.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.