SECTOR OF A CIRCLE

A part of the interior of a circle enclosed by an arc and two radii is called a sector of a given circle. 

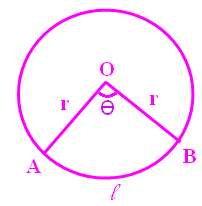
Consider a sector of a circle whose central angle measure. ∠AOB = θ and radius "r" and length of arc AB is known as L.

Area of sector

When we know the radius "r" of the circle and central angle "θ" of the sector : 

Area of the sector  =  (θ/360°) ⋅ Π r ²

When we know the radius "r" of the circle and arc length "l": 

Area of the sector = (l ⋅ r) / 2 

Arc length of sector

The formula to find the arc length is

=  (Arc Measure / 360°) ⋅ 2Π r

Major and minor sectors

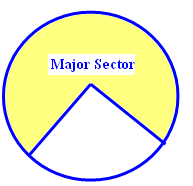
Major sector :

A larger part occupied by two radii is called the major sector. A major sector has central angle which is more than 180°.

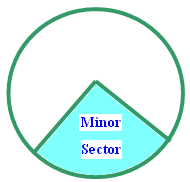
Minor sector :

A smaller part occupied by two radii is called the minor sector. A minor sector has central angle which is less than 180°.

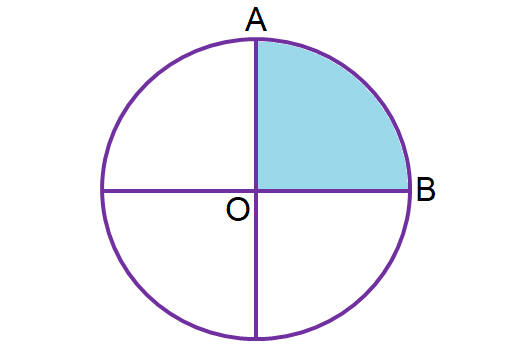
Quadrant :

A part occupied by two radii with central angle 90° is called quadrant. In other words we can define quadrant as one fourth of the circle.

Semicircle :

A part occupied by two radii with central angle 180° is called the semicircle.

Now we are going to have a set of question in which you have to choose which is major sector and which is minor sector. 

Sector of a circle - Examples

Question 1 :

Find the area of the sector whose radius and central angle are 42 cm and 60° respectively. (Take ∏  =  3.14 and round your answer to one decimal place, if necessary)

Solution :

The formula to find area of the sector is

=  (θ / 360°) ⋅ Π r²

Plug r  =  42, θ  =  60° and Π  ≈  3.14

≈  (60° / 360°) ⋅ 3.14 ⋅ 42²

≈  923. 2

Hence, the area of the sector is about 923.2 cm².

Question 2 :

Find the length of the arc that is bolded. (Take ∏  ≈  3.14 and round your answer to one decimal place, if necessary)

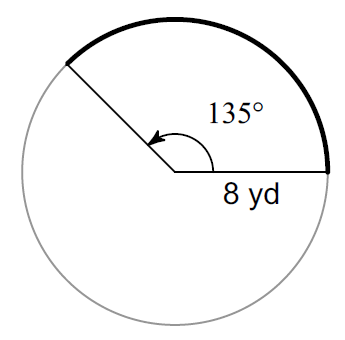
Solution :

The formula to find the arc length is

=  (Arc Measure / 360°) ⋅ 2Π r

Plug r  =  8, Arc Measure  =  135° and Π  ≈  3.14

≈  (135° / 360°) ⋅ 2 ⋅ 3.14 ⋅ 8

≈  18.9

Hence, the length of the arc is about 18.9 yd.

Question 3 :

Find the perimeter of sector whose area is 324 square cm and the radius is 27 cm.

Solution :

To find perimeter of sector, we need length of arc and radius of sector.

In the given question, we have radius but we don't have arc length. 

In order to find the arc length, let us use the formula (1/2) L r instead of area of sector.

Area of sector  =  324 cm²

(1/2) l ⋅ r

here r  =  27 cm

(1/2) ⋅ l ⋅ 27  =  324

                       l  =  (324 ⋅ 2)/27

                       l  =  12 ⋅ 2

                       L  =  24 cm

Now we may find the perimeter.

Perimeter of sector = L + 2r

  =  24 + 2(27)

  =  24 + 54

  =  78 cm 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.