SEGMENT AND ANGLE BISECTORS WORKSHEET

Problem 1 :

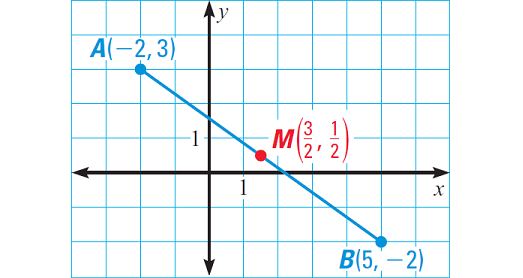
Find the coordinates of the midpoint of AB with endpoints A(-2, 3) and B(5, -2).

Problem 2 :

The midpoint of RP is M(2, 4). If one of the end points is R(-1, 7), find the coordinates of the other end point.

Problem 3 :

The ray FH bisects the angle ∠EFG. Given that m∠EFG = 120°, what are the measures of ∠EFH and ∠HFG ?

Problem 4 :

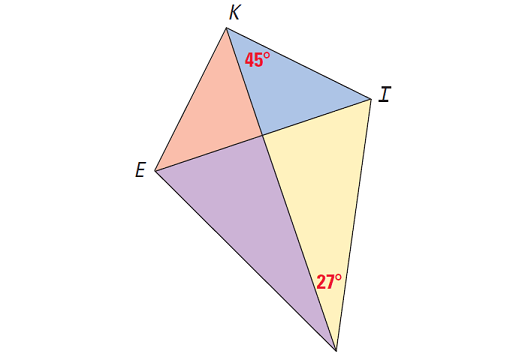
In the kite shown below, two angles are bisected.

∠EKI is bisected by KT

∠ITE is bisected by TK

Find the measures of the two angles.

Problem 5 :

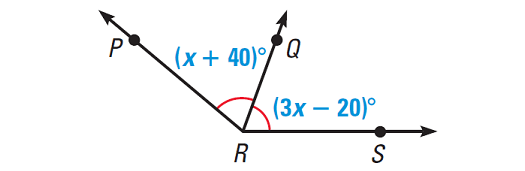
In the diagram shown below, RQ bisects ∠PRS. The measures of the two congruent angles are (x + 40)° and (3x - 20)°. Solve for x.

1. Answer :

Use the midpoint formula.

Here,

(x₁, y₁) = A(-2, 3)

(x₂, y₂) = B(5, -2)

Then, the midpoint of AB is

= [(-2 + 5)/2, (3 - 2)/2]

= (3/2, 1/2)

It has been illustrated in the picture given below.

2. Answer :

Let (a, b) be the coordinates of P.

Given :

Midpoint of RP = (2, 4)

[(x₁ + x₂)/2, (y₁ + y₂)/2] = (2, 4) ----(1)

Here,

(x₁, y₁) = R(-1, 7)

(x₂, y₂) = P(a, b)

Then, we have

(1)----> [(-1 + a)/2, (7 + b)/2] = (2, 4)

Equate the coordinates of x and y.

(-1 + a)/2 = 2  and  (7 + b)/2 = 4

-1 + a = 4  and 7 + b = 8

a = 5  and  b = 1

So, the other end point of the segment is P(5, 1).

3. Answer :

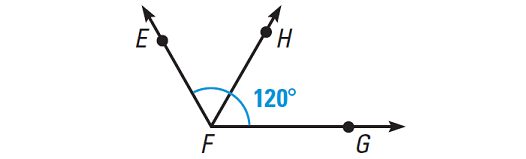
An angle bisector divides an angle into two congruent angles, each of which has half the measure of the original angle. So,

m∠EFH = m∠HFG

= 120°/2

= 60°

4. Answer :

We are given the measure of one of the two congruent angles that make up the larger angle. We can find the measure of the larger angle by doubling the measure of the smaller angle.

m∠EKI = 2m∠TKI

= 2(45°)

= 90°

m∠ITE = 2m∠KTI

= 2(27°)

= 54°

5. Answer :

Congruent angles have equal measures.

m∠PRQ = m∠QRS

Substitute given measures.

(x + 40)° = (3x - 20)°

Add 20° to each side.

x + 60 = 3x

Subtract x from each side.

60 = 2x

Divide each side by 2.

30 = x

So, x = 30. We can check by substituting to see that each of the congruent angles has a measure of 70°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.