SEGMENT LENGTHS IN CIRCLES

In this section, you will learn about the relationships that segments in circles have with each other. By definition, a segment is a part of a line. There are several different types of segments that we can have when it comes to circles. 

Finding Lengths of Segments of Chords

When two chords intersect in the interior of a circle, each chord is divided into two segments which are called segments of a chord.  The following theorem gives a relationship between the lengths of the four segments that are formed.

Theorem :

If two chords intersect in the interior of a circle, then the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord.

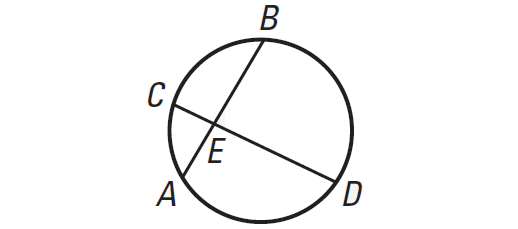
In the diagram, we have 

EA ⋅ EB  =  EC ⋅ ED

Proof of the above Theorem :

We can use similar triangles to prove the Theorem. 

Given : AB, CD are chords that intersect at E.

To Prove : EA · EB =  EC · ED

Draw DB and AC.  Because  m∠C and m∠B intercept the same are   ∠C  ≅  ∠B.  Likewise  ∠A  ≅  ∠D. 

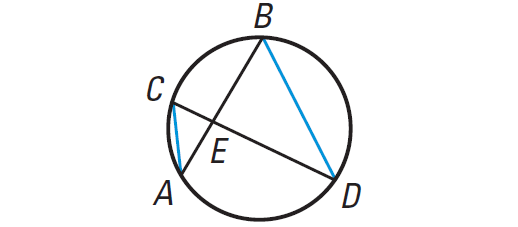
By the AA Similarity Postulate.  ∆AEC ∼ ∆DEB. 

So, the lengths of corresponding sides are proportional.

EA/ED  =  EC/EB

EA ⋅ EB  =  EC ⋅ ED

Finding Segment Lengths

Example 1 :

Chords ST and PQ intersect inside the circle.  Find the value of x.

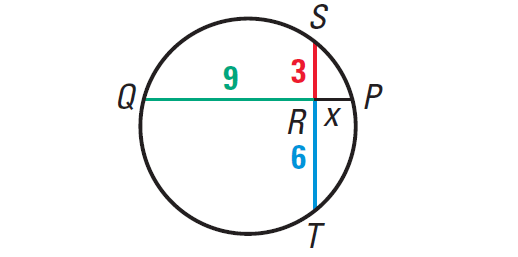
Solution :

Using the above Theorem, we have 

RQ · RP  =  RS · RT

Substitute.

9 · x  =  3 · 6

9x  =  18

Divide each side by 9. 

9x/9  =  18/9

x  =  2

Using Segments of Tangents and Secants

In the diagram shown below, PS is called a tangent segment because it is tangent to the circle at an endpoint.  Similarly, PR is a secant segment and PQ is the external segment of PR.

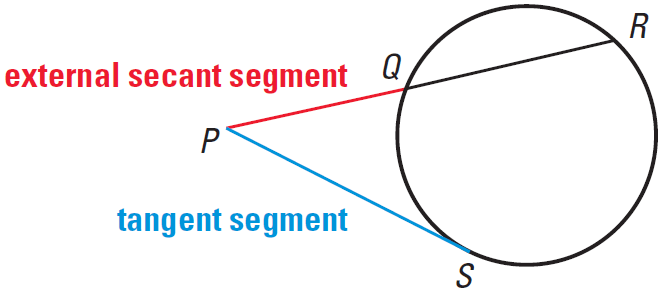
Theorem 1 :

If two secant segments share the same endpoint outside a circle, then the product of the length of one secant segment and the length of its external segment equals the product of the length of the other secant segment and the length of its external segment.

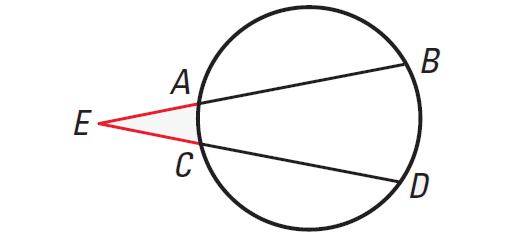
In the diagram shown above, we have

EA ⋅ EB  =  EC ⋅ ED

Theorem 2 :

If a secant segment and a tangent segment share an endpoint outside a circle, then the product of the length of the secant segment and the length of its external segment equals the square of the length of the tangent segment.

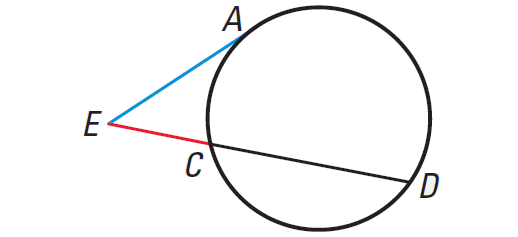
In the diagram shown above, we have

(EA)²  =  EC ⋅ ED

Finding Segment Lengths

Example 2 :

Find the value of x in the diagram shown below. 

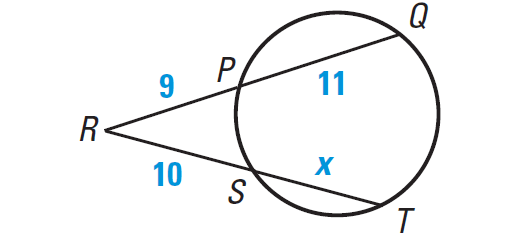
Solution :

Using Theorem, we have

RP · RQ  =  RS · RT

Substitute. 

9 · (11 + 9)  =  10 · (x + 10)

Simplify. 

180  =  10x + 100

Subtract 100 from each side. 

80  =  10x

Divide each side by 10.

80/10  =  10x/10

8  =  x

Example 3 :

Find the value of x in the diagram shown below. 

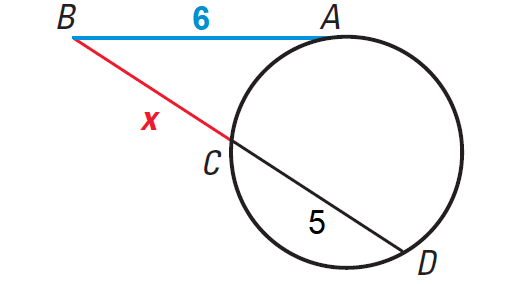
Solution :

Using Theorem, we have

(BA)²  =  BC · BD

Substitute. 

6²  =  x · (x + 5)

Simplify. 

36  =  x² + 5x

Subtract 36 from each side. 

0  =  x² + 5x - 36

or

x² + 5x - 36  =  0

Factor. 

(x + 9)(x - 4)  =  0

x + 9  =  0        or        x - 4  =  0

x  =  - 9        or        x  =  4

We can use only positive value for x. because lengths cannot be negative. 

So, we have

x  =  4

Estimating the Radius of a Circle

Example 4 :

You are standing at point C,  about 8 feet from a circular aquarium tank.  The distance from you to a point of tangency on the tank is about 20 feet.  Estimate the radius of the tank.

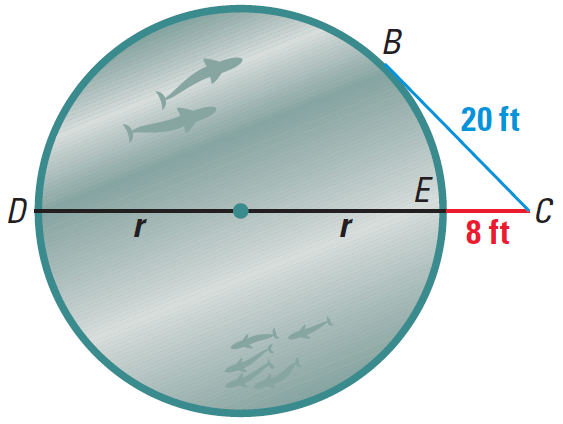
Solution :

Using Theorem, we have

(CB)²  =  CE · CD

Substitute.

20²  ≈  8 · (2r + 8)

Simplify.

400  ≈  16r + 64

Subtract 64 from each side. 

336  ≈  16r

Divide each side by 16. 

336/16  ≈  16r/16

21  ≈  r

Hence, the radius of the tank is about 21 feet. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.