SET THEORY WORD PROBLEMS AND SOLUTIONS WITH 2 CIRCLES

Problem 1 :

In a class, all students take part in either music or drama or both. 25 students take part in music, 30 students take part in drama and 8 students take part in both music and drama. Find

(i) The number of students who take part in only music.

(ii) The number of students who take part in only drama.

(iii) The total number of students in the class.

Solution :

Let "A" and "B" represents the students who participated music and drama respectively.

n(A)  =  25

n(B)  =  30

n(A n B)  =  8

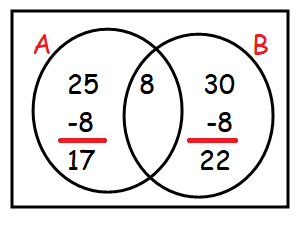
(i) The number of students who take part in only music

=  17

(ii) The number of students who take part in only drama

=  22

(iii) The total number of students in the class

  =  17 + 8 + 22

  =  47

Problem 2 :

In a party of 45 people, each one likes tea or coffee or both. 35 people like tea and 20 people like coffee. Find the number of people who (i) like both tea and coffee. (ii) do not like Tea. (iii) do not like coffee.

Solution :

Let "A" and "B" represents the people who drink tea and coffee respectively. 

n(A)  =  35

n(B)  =  20

n(A U B)  =  45

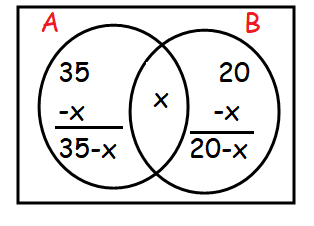
Total number of students  =  35 - x + x + 20 - x

55 - x  =  45

 -x  =  4 - 55

x  =  10

(i) like both tea and coffee  =  10

(ii) do not like Tea  =  20 - x (like coffee)

  =  20 - 10 

  =  10

(iii) do not like coffee  =  35 - x

  =  35 - 10 

  =  25

Problem 3 :

In an examination 50% of the students passed in Mathematics and 70% of students passed in Science while 10% students failed in both subjects. 300 students passed in both the subjects. Find the total number of students who appeared in the examination, if they took examination in only two subjects

Solution :

Number of students passed in both the subjects  =  300

Percentage of students passed in math  =  50% 

Percentage of students passed in science  =  70%

Percentage of students failed  =  10%

Percentage of students passed  =  90%

percentage of students passed in atleast one subject

  =  (50 + 70) - 90

  =  120 - 90

  =  30%

30% of x  =  300

x  =  300(100/30)

x  =  1000

So, the total number of students is 1000.

Problem 4 :

A and B are two sets such that n(A – B) = 32 + x, n(B – A) = 5x and n(A∩B) = x. Illustrate the information by means of a Venn diagram. Given that n(A) = n(B), calculate the value of x.

Solution :

Formulas for n(A) and n(B):

n(A)  =  n(A–B) + n(A∩B)

n(B)  =  n(B–A) + n(A∩B)

n(A – B) = 32 + x, n(B – A) = 5x and n(A∩B) = x

n(A)  =  32 + x + x

n(A)  =  32 + 2x  ----(1)

n(B)  =  5x + x

n(B)  =  6x  ------(2)

(1)  =  (2)

32 + 2x  =  6x

32  =  6x - 2x

4x  =  32

x  =  8

Problem 5 :

Th Venn diagram alongside illustrates the number of students in a particular class who study Chemistry (C) and History (H).

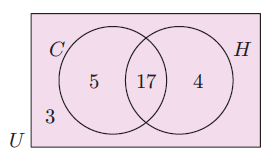
Determine the number of students:

a) in the class

b) who study both subjects

c) who study at least one of the subjects

d) who only study Chemistry.

Solution :

a) Total number of students in the class

= 3 + 5 + 17 + 4

= 29

b) Number of students who study both subjects is 17.

c) Number of students who study at least one of the subjects

= 5 + 17 + 4

= 26 students

who study at least one of the subjects

d) Number of students who study only chemistry is 5.

Problem 6 :

In a class of 30 students, 19 study Physics, 17 study Chemistry, and 15 study both of these subjects.

Display this information on a Venn diagram and hence determine the probability that a randomly selected class member studies:

a) both subjects

b) at least one of the subjects

c) Physics but not Chemistry

d) exactly one of the subjects

e) neither subject

Solution :

Displaying information :

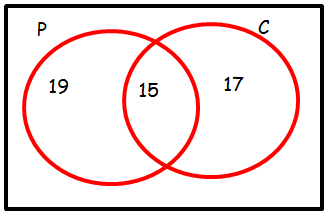
a) Number of students who study both subjects = 15

b) Number of students who study at least one of the subjects 

= (19-15) + 15 + (17 - 15)

= 4 + 15 + 2

= 21

Required probability = 21/30

c) Number of students who study physics but not chemistry

= 19 - 15

= 4

Required probability = 4/30

d) Number of students who study exactly one subject 

= (19 - 15) + (17 - 15)

= 4 + 2

= 6

Required probability = 6/30

e) Number of students who student neither subject

= Total number of students - number of students who study at least one subject

= 30 - 21

= 9 students.

Required probability = 9/30

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.