SIMILAR POLYGONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Identifying Similar Polygons
When there is a correspondence between two polygons such that their corresponding angles are congruent and the lengths of corresponding sides are proportional the two polygons are called similar polygons.
In the diagram shown below, PQRS is similar to WXYZ. The symbol ∼ is used to indicate similarity.
So, we have
PQRS ∼ WXYZ
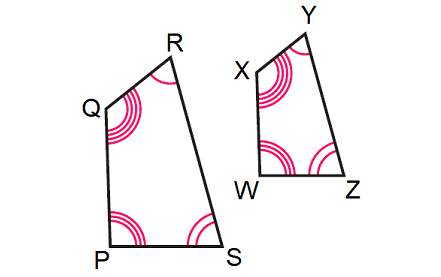
In the diagram shown above, because PQRS is similar to WXYZ, we have
Similar Polygons - Theorem
If two polygons are similar, then the ratio of their perimeters is equal to the ratios of their corresponding side lengths.
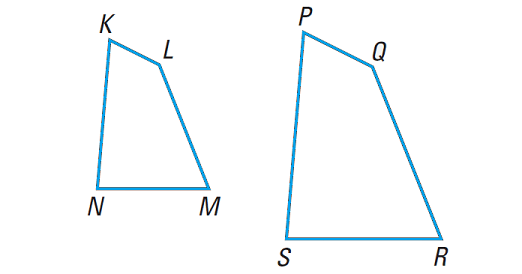
In the diagram shown above, if KLMN ∼ PQRS, then
Writing Similarity Statements
Example 1 :
Pentagons JKLMN and STUVW shown below are similar. List all the pairs of congruent angles. Write the ratios of the corresponding sides in a statement of proportionality.
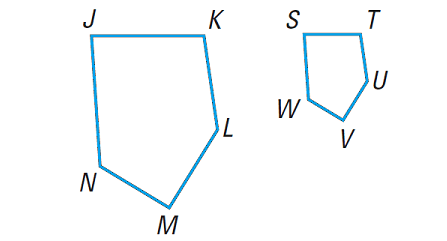
Solution :
Because JKLM ∼ STUVW, we can write
∠J ≅ ∠S
∠K ≅ ∠T
∠L ≅ ∠U
∠M ≅ ∠V
∠N ≅ ∠W
We can write the statement of proportionality as follows :
JK/ST = KL/TU = LM/UV = MN/VW = NJ/WS
Comparing Similar Polygons
Example 2 :
Decide whether the figures are similar. If they are similar, write a similarity statement.
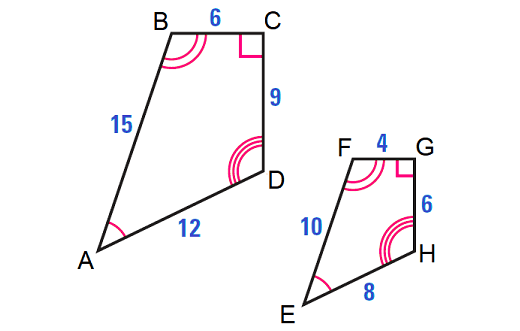
As shown, the corresponding angles of ABCD and EFGH are congruent. Also, the corresponding side lengths are proportional.
AB/EF = 15/10 = 3/2
BC/FG = 6/4 = 3/2
CD/GH = 9/6 = 3/2
DA/HE = 12/8 = 3/2
Hence, the two figures are similar and we can write
ABCD ∼ EFGH
Note :
If two polygons are similar, then the ratio of the lengths of two corresponding sides is called the scale factor. In the above example, the common ratio is 3/2 is the scale factor of ABCD to EFGH.
Comparing Photographic Enlargements
Example 3 :
We are asked to create a poster to advertise a field trip to see the Liberty Bell. We have a 3.5 inch by 5 inch photo that you want to enlarge. We want the enlargement to be 16 inches wide. How long will it be ?
Solution :
To find the length of the enlargement, you can compare the enlargement to the original measurements of the photo.

From the diagram shown above, we have
x/5 = 16/3.5
Multiply both sides by 5.
x = 16/0.7
x ≈ 22.9 in.
Hence, the length of the enlargement will be about 23 inches.
Using Similar Polygons
Example 4 :
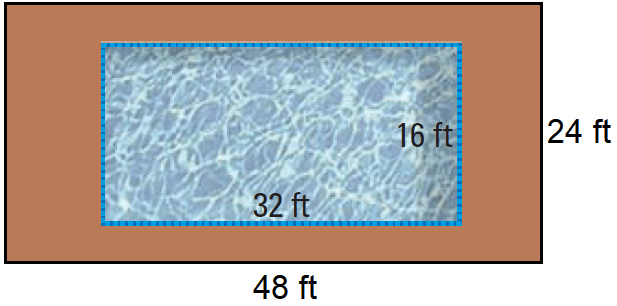
The rectangular patio around a pool is similar to the pool as shown below. Calculate the scale factor of the patio to the pool, and find the ratio of their perimeters.
Solution :
Because the rectangles are similar, the scale factor of the patio to the pool is 48 : 32, which is 3 : 2 in simplified form.
The perimeter of the patio is
2(24) + 2(48) = 144 feet
and the perimeter of the pool is
2(16) + 2(32) = 96 feet.
The ratio of the perimeters is
= 144/96
= 3/2
In similar figures, the ratio of the perimeters is the same as the scale factor.
So, the scale factor of the patio to the pool is 3/2.
Example 5 :
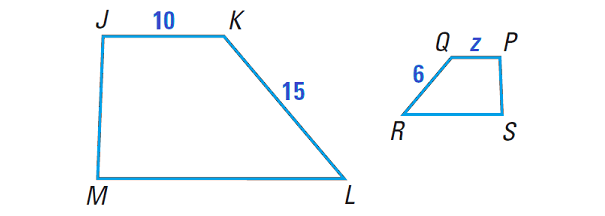
In the diagram shown below, quadrilateral JKLM is similar to quadrilateral PQRS. Find the value of z.
Solution :
Because the quadrilaterals JKLM is similar to PQRS, we can set up the proportion that contains PQ.
Write proportion :
KL/QR = JK/PQ
Substitute.
15/6 = 10/z
5/2 = 10/z
Using reciprocal property,
2/5 = z/10
Multiply each side by 10.
2(2) = z
4 = z
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact US | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 39)
Dec 11, 25 05:59 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation

